Strukturierte Daten für Matherechner (`MathSolver`)

Mit strukturierten Daten kannst du Schüler, Lehrer und andere Nutzer bei mathematischen Problemen unterstützen. Gib dazu die Art der jeweiligen mathematischen Aufgabe und Links zu Schritt-für-Schritt-Anleitungen für bestimmte mathematische Probleme an. Das folgende Beispiel zeigt, wie Matherechner in den Google-Suchergebnissen erscheinen können (die Darstellung kann sich ändern):

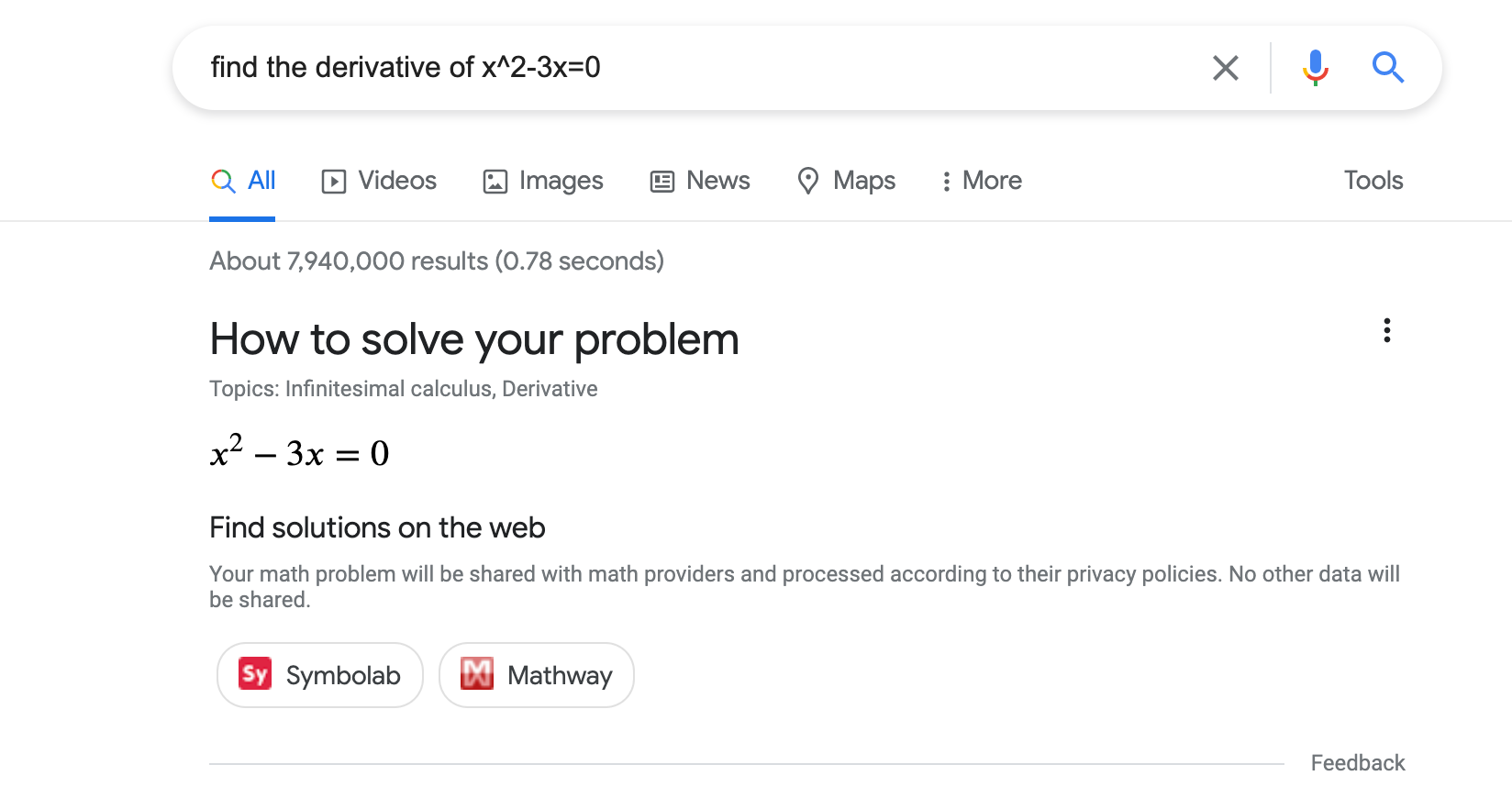
$Beispiel für ein Rich-Suchergebnis für Matherechner$

So fügst du strukturierte Daten hinzu

Strukturierte Daten sind ein standardisiertes Format, mit dem du Informationen zu einer Seite angeben und die Seiteninhalte klassifizieren kannst. Falls strukturierte Daten für dich ein neues Thema sind, findest du hier Informationen dazu, wie sie funktionieren.

In der folgenden Übersicht haben wir zusammengefasst, wie du strukturierte Daten erstellst, testest und veröffentlichst. Eine detaillierte Anleitung dazu, wie du einer Webseite strukturierte Daten hinzufügst, findest du im Codelab zu strukturierten Daten.

Füge die erforderlichen Properties hinzu. Hier erfährst du, wie du strukturierte Daten je nach verwendetem Format auf der Seite einfügst.
Verwendest du ein CMS? Möglicherweise ist es einfacher, ein Plug-in zu verwenden, das in dein CMS eingebunden ist.
Verwendest du JavaScript? Hier erfährst du, wie du strukturierte Daten mit JavaScript generierst.
Folge den Richtlinien.
Prüfe deinen Code mit dem Test für Rich-Suchergebnisse und behebe alle kritischen Fehler. Zusätzlich solltest du alle nicht kritischen Probleme beheben, die im Tool möglicherweise gemeldet werden. Das kann dabei helfen, die Qualität deiner strukturierten Daten zu verbessern. Das ist jedoch nicht nötig, um für Rich-Suchergebnisse geeignet zu sein.
Stelle ein paar Seiten mit deinen strukturierten Daten bereit und teste mit dem URL-Prüftool, wie Google die Seiten sieht. Achte darauf, dass die Seiten für Google zugänglich sind und nicht durch eine robots.txt-Datei, das noindex-Tag oder Anmeldeanforderungen blockiert werden. Wenn die Seiten in Ordnung sind, kannst du Google bitten, deine URLs noch einmal zu crawlen.
Hinweis: Gib Google etwas Zeit, die Seiten neu zu crawlen und zu indexieren. Nachdem eine Seite veröffentlicht wurde, kann es einige Tage dauern, bis sie von Google gefunden und gecrawlt wurde.
Damit Google über künftige Änderungen auf dem Laufenden bleibt, empfehlen wir dir, eine Sitemap einzureichen. Mit der Search Console Sitemap API lässt sich dieser Vorgang automatisieren.

Beispiele

Ein Matherechner

Hier siehst du ein Beispiel für eine Startseite mit einem Matherechner, der Aufgaben mit Polynomgleichungen und Ableitungen bearbeiten kann, und auf Englisch und Spanisch verfügbar ist.

<html>
<head>
<title>An awesome math solver</title>
</head>
<body>
<script type="application/ld+json">
[
  {
    "@context": "https://schema.org",
    "@type": ["MathSolver", "LearningResource"],
    "name": "An awesome math solver",
    "url": "https://www.mathdomain.com/",
    "usageInfo": "https://www.mathdomain.com/privacy",
    "inLanguage": "en",
    "potentialAction": [{
      "@type": "SolveMathAction",
      "target": "https://mathdomain.com/solve?q={math_expression_string}",
      "mathExpression-input": "required name=math_expression_string",
      "eduQuestionType": ["Polynomial Equation","Derivative"]
     }],
    "learningResourceType": "Math solver"
  },
  {
    "@context": "https://schema.org",
    "@type": ["MathSolver", "LearningResource"],
    "name": "Un solucionador de matemáticas increíble",
    "url": "https://es.mathdomain.com/",
    "usageInfo": "https://es.mathdomain.com/privacy",
    "inLanguage": "es",
    "potentialAction": [{
      "@type": "SolveMathAction",
      "target": "https://es.mathdomain.com/solve?q={math_expression_string}",
      "mathExpression-input": "required name=math_expression_string",
      "eduQuestionType": ["Polynomial Equation","Derivative"]
     }],
    "learningResourceType": "Math solver"
  }
]
</script>
</body>
</html>

<html>
<head>
<title>An awesome math solver</title>
</head>
<body>
<script type="application/ld+json">
[
  {
    "@context": "https://schema.org",
    "@type": ["MathSolver", "LearningResource"],
    "name": "An awesome math solver",
    "url": "https://www.mathdomain.com/",
    "usageInfo": "https://www.mathdomain.com/privacy",
    "inLanguage": "en",
    "potentialAction": [{
      "@type": "SolveMathAction",
      "target": "https://mathdomain.com/solve?q={math_expression_string}",
      "mathExpression-input": "required name=math_expression_string",
      "eduQuestionType": ["Polynomial Equation","Derivative"]
     }],
    "learningResourceType": "Math solver"
  },
  {
    "@context": "https://schema.org",
    "@type": ["MathSolver", "LearningResource"],
    "name": "Un solucionador de matemáticas increíble",
    "url": "https://es.mathdomain.com/",
    "usageInfo": "https://es.mathdomain.com/privacy",
    "inLanguage": "es",
    "potentialAction": [{
      "@type": "SolveMathAction",
      "target": "https://es.mathdomain.com/solve?q={math_expression_string}",
      "mathExpression-input": "required name=math_expression_string",
      "eduQuestionType": ["Polynomial Equation","Derivative"]
     }],
    "learningResourceType": "Math solver"
  }
]
</script>
</body>
</html>

Das spanische Markup könnte direkt in https://es.mathdomain.com/ und nicht neben der englischen Version des Matherechner-Markups platziert werden.

Zwei Matherechner

Dieses Beispiel zeigt eine Startseite mit zwei Matherechnern: Ein Endpunkt kann Polynomgleichungen, der andere trigonometrische Gleichungen bearbeiten. Die Seite ist nur auf Englisch verfügbar.

<html>
<head>
<title>An awesome math solver</title>
</head>
<body>
<script type="application/ld+json">
{
  "@context": "https://schema.org",
  "@type": ["MathSolver", "LearningResource"],
  "name": "An awesome math solver",
  "url": "https://www.mathdomain.com/",
  "usageInfo": "https://www.mathdomain.com/privacy",
  "inLanguage": "en",
  "potentialAction": [{
     "@type": "SolveMathAction",
     "target": "https://mathdomain.com/solve?q={math_expression_string}",
     "mathExpression-input": "required name=math_expression_string",
     "eduQuestionType": "Polynomial Equation"
   },
   {
     "@type": "SolveMathAction",
     "target": "https://mathdomain.com/trig?q={math_expression_string}",
     "mathExpression-input": "required name=math_expression_string",
     "eduQuestionType": "Trigonometric Equation"
   }],
  "learningResourceType": "Math solver"
}
</script>
</body>
</html>

Richtlinien

Damit deine Seite als Rich-Suchergebnis für Matherechner dargestellt werden kann, musst du folgende Richtlinien beachten:

Technische Richtlinien

Füge der Startseite deiner Website strukturierte MathSolver-Daten hinzu.
In deinen Hostlast-Einstellungen muss eine hohe Crawling-Frequenz konfiguriert sein.
Wenn mehrere identische Kopien desselben Matherechners unter verschiedenen URLs gehostet werden, verwende die kanonischen URLs auf jeder Kopie der Seite.
Matherechner, die nur nach Anmeldung vollständig zugänglich oder gänzlich hinter einer Paywall verborgen sind, sind nicht zulässig. Sobald Nutzer von der Funktion auf Google zu deiner Website gehen, müssen sie auf die Lösung und eine Schritt-für-Schritt-Anleitung für ihr ursprüngliches Problem zugreifen können. Zulässig ist es jedoch, für den Zugang zu zusätzlichen Inhalten eine Anmeldung zu verlangen oder solche Inhalte hinter einer Paywall zu verbergen.

Inhaltsrichtlinien

Wir haben diese Inhaltsrichtlinien für Matherechner erstellt, damit unsere Nutzer relevante Lernressourcen finden können. Wenn wir Inhalte finden, die gegen diese Richtlinien verstoßen, reagieren wir entsprechend. Unter anderem können wir manuelle Maßnahmen ergreifen und deine Seiten aus der Funktion für Matherechner bei Google entfernen.

Wir erlauben keine Werbung, die als Matherechner ausgegeben wird, wie Inhalte von Drittanbietern (beispielsweise Affiliate-Programme).
Du bist selbst für die inhaltliche Korrektheit und die Qualität deines Matherechners verantwortlich. Wenn ein bestimmter Teil deiner Daten im Rahmen unserer Qualitätsprüfungen als nicht korrekt eingestuft wird, kann dein Rechner unter Umständen aus der Funktion entfernt werden, bis du die Probleme behoben hast. Ob es zu einer Entfernung kommt, hängt davon ab, wie schwerwiegend die Probleme sind. Dies gilt für:
- Die Genauigkeit der Problemtypen, die der Rechner lösen kann.
- Die Genauigkeit deiner Lösungen für mathematische Probleme, bei denen der Rechner angibt, dass er sie lösen kann.

Definitionen strukturierter Datentypen

Damit die Inhalte als Rich-Suchergebnis angezeigt werden können, musst du alle erforderlichen Properties hinzufügen. Du kannst auch die empfohlenen Properties einbinden, um deine strukturierten Daten weiter zu ergänzen und damit deinen Nutzern Mehrwert zu bieten.

MathSolver

Ein MathSolver ist ein Tool, das Schüler, Lehrer und andere Nutzer mit Schritt-für-Schritt-Lösungen bei der Bearbeitung von Matheaufgaben unterstützt. Verwende strukturierte MathSolver-Daten auf der Startseite deiner Website.

Die vollständige Definition von MathSolver findest du unter schema.org/MathSolver.

Die von Google unterstützten Properties sind folgende:

Erforderliche Properties
`potentialAction`	`SolveMathAction` Die Aktion, die zur Erklärung eines mathematischen Ausdrucks führt (z. B. in Form einer Schritt-für-Schritt-Lösung oder eines Diagramms). { "@type": "MathSolver", "potentialAction": [{ "@type": "SolveMathAction", "target": "https://mathdomain.com/solve?q={math_expression_string}", "mathExpression-input": "required name=math_expression_string", "eduQuestionType": "Polynomial Equation" }] }
`potentialAction.mathExpression-input`	`Text` Ein Platzhalter für einen mathematischen Ausdruck (z. B. x^2 – 3x = 0), der von Google an deine Website gesendet wird. Du kannst dann den mathematischen Ausdruck „lösen“. Dies kann das Vereinfachen, Umwandeln oder Auflösen nach einer bestimmten Variablen bedeuten. Dieser String kann viele Formate haben, z. B. LaTeX, Ascii-Math oder mathematische Ausdrücke, die auf einer Tastatur geschrieben werden können. `mathExpression-input` ist eine annotierte Property. Weitere Informationen findest du auf dieser Seite: `Potential Actions`. Bei einigen Problemtypen gibt `math_expression_string` sowohl den Problemtyp als auch die Parameter des Problemtyps an. Im Folgenden findest du einige Beispiele für komplexere Problemtypen, damit du sie antizipieren und richtig parsen kannst. Derivate Google sendet einen `math_expression_string` in einer der beiden folgenden Formen: (`math_expression`)' d/d`variable` `math_expression` Beispiele: `(x^2+x)'` `d/dx (x^2+x)` `d/dy y^2+y` Integrale Google sendet einen `math_expression_string` in einer der beiden folgenden Formen: \int `math_expression` \int_{`from`}^{`to`} `math_expression` Beispiele: `\int x^2+x` `\int_{0}^{2} x^2+x` Einschränkungen Google sendet einen `math_expression_string` in einer der beiden folgenden Formen: \lim `math_expression` \lim_{`variable`\rightarrow`value`} `math_expression` Beispiele: `\lim_{x\rightarrow0} sin(x)/x` `\lim_{y\rightarrow\infty} sin(y)/y` `\lim sin(x)/x`
`url`	`URL` Die URL von `MathSolver`.
`usageInfo`	`URL` Die Datenschutzerklärung deiner Website für mathematische Aufgaben. { "@type": "MathSolver", "usageInfo": "https://www.mathdomain.com/privacy" }
`potentialAction.target`	`EntryPoint` Der Einstiegspunkt der URL-Ausrichtung für eine Aktion. Die Property `potentialAction.target` akzeptiert einen String, um den mathematischen Ausdruck darzustellen, der durch die Aktion bearbeitet wird. { "@type": "MathSolver", "potentialAction": [{ "@type": "SolveMathAction", "target": "https://mathdomain.com/solve?q={math_expression_string}" }] }

Empfohlene Properties

Empfohlene Properties
`inLanguage`	`Text` Die Sprachen, die von deiner Website für mathematische Aufgaben unterstützt werden. Eine Liste der möglichen Sprachen findest du in dieser Tabelle. { "@type": "MathSolver", "inLanguage": "es" }
`assesses`	`Text`-Liste mit den Definitionen der Problemtypen Problemtypen, die mit `HowTo` behoben werden. Verwende die Property `assesses`, wenn du `HowTo`-Markup zusätzlich zum `MathSolver`-Markup nutzt. { "@type": "MathSolver", "assesses": "Polynomial Equation" }
`potentialAction.eduQuestionType`	`Text`-Liste mit den Definitionen der Problemtypen Problemtypen, die von der Property `potentialAction.target` gelöst werden können. { "@type": "SolveMathAction", "eduQuestionType": "Polynomial Equation" }

inLanguage

Text

Die Sprachen, die von deiner Website für mathematische Aufgaben unterstützt werden. Eine Liste der möglichen Sprachen findest du in dieser Tabelle.


{
  "@type": "MathSolver",
  "inLanguage": "es"
}

assesses

Text-Liste mit den Definitionen der Problemtypen

Problemtypen, die mit HowTo behoben werden. Verwende die Property assesses, wenn du HowTo-Markup zusätzlich zum MathSolver-Markup nutzt.


{
  "@type": "MathSolver",
  "assesses": "Polynomial Equation"
}

potentialAction.eduQuestionType

Text-Liste mit den Definitionen der Problemtypen

Problemtypen, die von der Property potentialAction.target gelöst werden können.


{
  "@type": "SolveMathAction",
  "eduQuestionType": "Polynomial Equation"
}

LearningResource

LearningResource gibt an, dass das Thema des Markups eine Ressource ist, die Schüler, Lehrer und andere Nutzer bei der Bearbeitung von Lerninhalten unterstützt. Verwende LearningResource auf der Startseite deiner Website.

Die vollständige Definition von LearningResource findest du unter schema.org/LearningResource.

Die von Google unterstützten Properties sind folgende:

Erforderliche Properties

Erforderliche Properties
`learningResourceType`	`Text` Typ dieser Lernressource. Verwende diesen festen Wert: `Math Solver`. { "@type": ["MathSolver", "LearningResource"], "learningResourceType": "Math Solver" }

learningResourceType