Dados estruturados de solucionador matemático (MathSolver)

Para ajudar alunos, professores e outras pessoas com problemas matemáticos, é possível usar dados estruturados para indicar o tipo de problema matemático e links para instruções passo a passo de problemas específicos. Veja um exemplo de como os solucionadores matemáticos podem aparecer nos resultados da Pesquisa Google (a aparência está sujeita a mudanças):

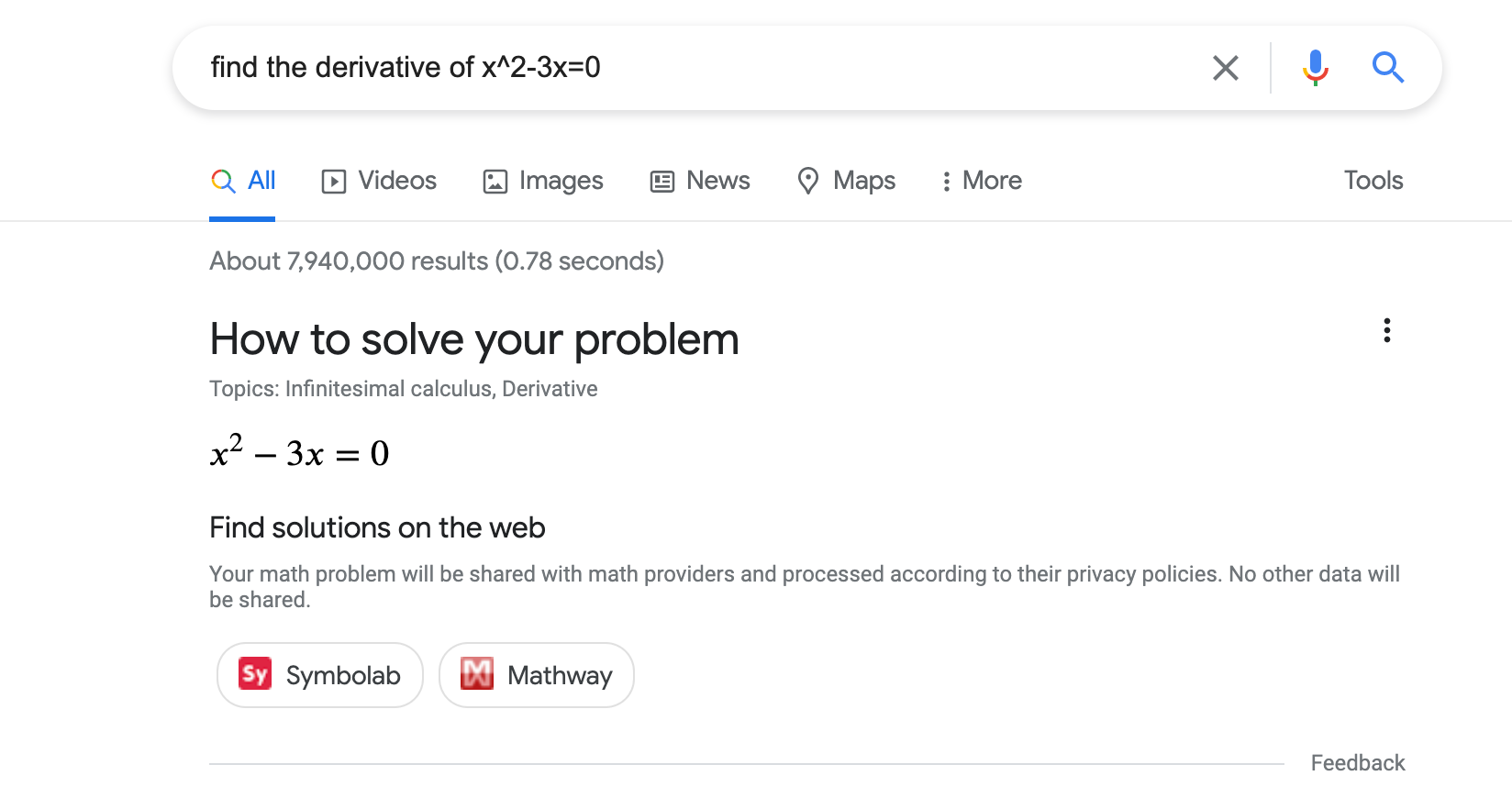
Exemplo de pesquisa aprimorada de solucionadores matemáticos

Como adicionar dados estruturados

Os dados estruturados são um formato padronizado para fornecer informações sobre uma página e classificar o conteúdo dela. Caso você não saiba muito sobre o assunto, veja como os dados estruturados funcionam.

Esta é uma visão geral de como criar, testar e lançar dados estruturados.

  1. Adicione as propriedades obrigatórias. Com base no formato que você está usando, saiba onde inserir dados estruturados na página.
  2. Siga as diretrizes.
  3. Valide o código com o Teste de pesquisa aprimorada e corrija os erros críticos. Corrija também os problemas não críticos que possam ser sinalizados na ferramenta, porque eles podem melhorar a qualidade dos dados estruturados, mas isso não é necessário para se qualificar para pesquisas aprimoradas.
  4. Implante algumas páginas que incluam os dados estruturados e use a Ferramenta de inspeção de URL para testar como o Google vê a página. Verifique se a página está acessível ao Google e se não está bloqueada por um arquivo robots.txt, pela tag noindex ou por requisitos de login. Se estiver tudo certo, peça ao Google para rastrear novamente seus URLs.
  5. Para informar o Google sobre mudanças futuras, recomendamos que você envie um sitemap. É possível automatizar isso com a API Search Console Sitemap.

Exemplos

Uma ação do solucionador

Veja um exemplo de página inicial de solucionador matemático, disponível em inglês e espanhol, com uma ação que pode resolver equações polinomiais e problemas de derivada.


<html>
<head>
<title>An awesome math solver</title>
</head>
<body>
<script type="application/ld+json">
[
  {
    "@context": "https://schema.org",
    "@type": ["MathSolver", "LearningResource"],
    "name": "An awesome math solver",
    "url": "https://www.mathdomain.com/",
    "usageInfo": "https://www.mathdomain.com/privacy",
    "inLanguage": "en",
    "potentialAction": [{
      "@type": "SolveMathAction",
      "target": "https://mathdomain.com/solve?q={math_expression_string}",
      "mathExpression-input": "required name=math_expression_string",
      "eduQuestionType": ["Polynomial Equation","Derivative"]
     }],
    "learningResourceType": "Math solver"
  },
  {
    "@context": "https://schema.org",
    "@type": ["MathSolver", "LearningResource"],
    "name": "Un solucionador de matemáticas increíble",
    "url": "https://es.mathdomain.com/",
    "usageInfo": "https://es.mathdomain.com/privacy",
    "inLanguage": "es",
    "potentialAction": [{
      "@type": "SolveMathAction",
      "target": "https://es.mathdomain.com/solve?q={math_expression_string}",
      "mathExpression-input": "required name=math_expression_string",
      "eduQuestionType": ["Polynomial Equation","Derivative"]
     }],
    "learningResourceType": "Math solver"
  }
]
</script>
</body>
</html>

Duas ações do solucionador

Veja um exemplo de página inicial de solucionador matemático com dois endpoints de resolução: um para resolver equações polinomiais e o outro para equações trigonométricas. O recurso está disponível apenas em inglês.


<html>
<head>
<title>An awesome math solver</title>
</head>
<body>
<script type="application/ld+json">
{
  "@context": "https://schema.org",
  "@type": ["MathSolver", "LearningResource"],
  "name": "An awesome math solver",
  "url": "https://www.mathdomain.com/",
  "usageInfo": "https://www.mathdomain.com/privacy",
  "inLanguage": "en",
  "potentialAction": [{
     "@type": "SolveMathAction",
     "target": "https://mathdomain.com/solve?q={math_expression_string}",
     "mathExpression-input": "required name=math_expression_string",
     "eduQuestionType": "Polynomial Equation"
   },
   {
     "@type": "SolveMathAction",
     "target": "https://mathdomain.com/trig?q={math_expression_string}",
     "mathExpression-input": "required name=math_expression_string",
     "eduQuestionType": "Trigonometric Equation"
   }],
  "learningResourceType": "Math solver"
}
</script>
</body>
</html>

Diretrizes

Se você quiser qualificar sua página para a pesquisa aprimorada de solucionador matemático, siga estas diretrizes:

Diretrizes técnicas

  • Adicione os dados estruturados MathSolver à página inicial do site.
  • Confira se o Googlebot pode rastrear seu site de modo eficiente.
  • Se você tiver várias cópias idênticas do mesmo solucionador matemático hospedadas em URLs diferentes, use os URLS canônicos em cada cópia da página.
  • Não permitimos solucionadores de matemática que estejam totalmente protegidos por login ou paywall. Depois que os usuários navegarem do recurso no Google até seu site, a solução e as instruções passo a passo referentes ao problema inicial precisarão estar acessíveis a eles. Conteúdo adicional pode ser protegido por login ou paywall.

Diretrizes de conteúdo

Criamos estas diretrizes de conteúdo de solucionadores matemáticos para garantir que nossos usuários encontrem recursos de aprendizado relevantes. Se encontrarmos conteúdo que viole essas políticas, responderemos adequadamente. Isso pode incluir ações manuais e a remoção das suas páginas da experiência de solucionadores matemáticos do Google.

  • Não permitimos conteúdo promocional disfarçado de solucionador matemático, como aqueles postados por terceiros (por exemplo, programas de afiliados).
  • Você é responsável pela precisão e qualidade dos solucionadores matemáticos oferecidos com esse recurso. Se uma determinada quantidade de dados for considerada imprecisa com base nos nossos processos de avaliação de qualidade, talvez os solucionadores sejam removidos do recurso até que os problemas sejam resolvidos, dependendo da gravidade. Isso se aplica ao seguinte:
    • A precisão dos tipos de problemas que o solucionador pode resolver
    • A precisão das soluções para problemas matemáticos que o solucionador declara conseguir resolver

Definições de tipos de dados estruturados

É necessário incluir as propriedades obrigatórias para que seu conteúdo seja qualificado para exibição na pesquisa aprimorada. Também é possível incluir as propriedades recomendadas para adicionar mais informações aos seus dados estruturados, o que pode proporcionar uma melhor experiência do usuário.

MathSolver

MathSolver é uma ferramenta que ajuda alunos, professores e outras pessoas a resolver problemas matemáticos com a criação de soluções passo a passo. Use dados estruturados MathSolver na página inicial do site.

A definição completa de MathSolver está disponível em schema.org/MathSolver (em inglês).

Confira as propriedades aceitas pelo Google:

Propriedades obrigatórias
potentialAction

SolveMathAction

É a ação que leva a uma explicação matemática (por exemplo, gráfico ou solução passo a passo) de uma expressão matemática.

{
"@type": "MathSolver",
"potentialAction": [{
  "@type": "SolveMathAction",
  "target": "https://mathdomain.com/solve?q={math_expression_string}",
  "mathExpression-input": "required name=math_expression_string",
  "eduQuestionType": "Polynomial Equation"
  }]
}
potentialAction.mathExpression-input

Text

Um marcador de posição para uma expressão matemática (por exemplo: x^2-3x=0) que é enviado pelo Google ao seu site. Assim, é possível "resolver" a expressão matemática, o que pode envolver simplificação, transformação ou resolução de uma variável específica. A string pode ter muitos formatos. Por exemplo: LaTeX, Ascii-Math ou expressões matemáticas que podem ser escritas com o teclado.

Em alguns casos, math_expression_string indica o tipo e os parâmetros do tipo de problema. Confira a seguir alguns exemplos mais complicados para que você possa antecipar e analisar os tipos de problemas corretamente.

Derivativos

O Google envia um math_expression_string de uma destas duas formas:

  • (math_expression)'
  • d/dvariable math_expression

Examples:

  • (x^2+x)'
  • d/dx (x^2+x)
  • d/dy y^2+y

Integrals

Google will send a math_expression_string in one of two forms:

  • \int math_expression
  • \int_{from}^{to} math_expression

Exemplos:

  • \int x^2+x
  • \int_{0}^{2} x^2+x

Limites

O Google envia um math_expression_string de uma destas duas formas:

  • \lim math_expression
  • \lim_{variable\rightarrowvalue} math_expression

Exemplos:

  • \lim_{x\rightarrow0} sin(x)/x
  • \lim_{y\rightarrow\infty} sin(y)/y
  • \lim sin(x)/x
url

URL

É o URL de MathSolver.
usageInfo

URL

É a Política de Privacidade do seu site de solução de problemas de matemática.

{
  "@type": "MathSolver",
  "usageInfo": "https://www.mathdomain.com/privacy"
}
potentialAction.target

EntryPoint

É o ponto de entrada de destino do URL para uma ação. A propriedade potentialAction.target aceita uma string para representar a expressão matemática sendo resolvida pela ação.

{
"@type": "MathSolver",
"potentialAction": [{
  "@type": "SolveMathAction",
  "target": "https://mathdomain.com/solve?q={math_expression_string}"
  }]
}
Propriedades recomendadas
inLanguage

Text

São os idiomas aceitos pelo site de resolução de problemas matemáticos. Consulte esta tabela para ver uma lista dos possíveis idiomas.

{
  "@type": "MathSolver",
  "inLanguage": "es"
}
assesses

Text: lista de definições de tipo de problema

São os tipos de problemas resolvidos com o HowTo. Use a propriedade assesses se estiver usando HowTo, além da marcação MathSolver.

{
  "@type": "MathSolver",
  "assesses": "Polynomial Equation"
}
potentialAction.eduQuestionType

Text: lista de definições de tipo de problema

São os tipos de problemas que podem ser resolvidos pela propriedade potentialAction.target.

{
  "@type": "SolveMathAction",
  "eduQuestionType": "Polynomial Equation"
}

LearningResource

LearningResource indica que o assunto da marcação é um recurso que ajuda alunos, professores e outras pessoas a aprender. Use LearningResource na página inicial do seu site.

A definição completa de LearningResource está disponível em schema.org/LearningResource (em inglês).

Confira as propriedades aceitas pelo Google:

Propriedades obrigatórias
learningResourceType

Text

É o tipo desse recurso de aprendizado. Use este valor fixo: Math Solver.

{
  "@type": ["MathSolver", "LearningResource"],
  "learningResourceType": "Math Solver"
}

Definições de tipo de problema

Use a lista de tipos de problemas a seguir como eduQuestionType para MathSolver.potentialAction ou para o campo assesses de um MathSolver quando MathSolver estiver acompanhando um HowTo que instrui sobre um problema matemático específico.

A tabela a seguir mostra alguns exemplos para os tipos de problemas que podem ser anotados:

Exemplos de tipos de problemas (não é uma lista completa)
Absolute Value Equation

Equações de valor absoluto. Por exemplo: |x - 5| = 9
Algebra

É um tipo de problema genérico que pode ser colocado com outro tipo de problema. Por exemplo: equações polinomiais, equações exponenciais e expressões radicais.
Arc Length

Problemas de comprimento do arco. Por exemplo: determinar o comprimento de x = 4 (3 + y)^2, 1 < y < 4.
Arithmetic

Problemas de aritmética. Por exemplo: encontrar a soma de 5 + 7.
Biquadratic Equation

Equações biquadradas. Por exemplo: x^4 - x^2 - 2 = 0.
Calculus

É um tipo de problema genérico que pode ser colocado com outros tipos de problema. Por exemplo: integrais, derivadas e equações diferenciais.
Characteristic Polynomial

Encontrar o polinômio característico de {{1,2,5}, {3,-1,1}, {1,2,3}}.
Circle

Problemas relacionados a círculos. Por exemplo: encontrar o raio de x^2 + y^2 = 3.
Derivative

Derivada de 5x^4 + 2x^3 + 4x - 2.
Differential Equation

Problemas de equação diferencial. Por exemplo: y+dy/dx=5x.
Distance

Problemas de distância. Por exemplo: encontrar a distância entre (6,-1) e (-3,2).
Eigenvalue

Problemas de valor próprio. Por exemplo: encontrar os valores próprios para a matriz [[-6, 3], [4, 5]].
Eigenvector

Problemas de vetores próprios. Por exemplo: encontrar o vetor próprio da matriz [[-6, 3], [4, 5]] com valores próprios [-7, 6].
Ellipse

Problemas de elipses. Por exemplo: encontrar as interseções em x e y de 9x^2 + 4y^2 = 36.
Exponential Equation

Equações exponenciais. Por exemplo: 7^x = 9.
Function

Simplificações polinomiais. Por exemplo: (x-5)^2 * (x+5)^2.
Function Composition

f(g(x)) quando f(x)=x^2-2x, g(x)=2x-2
Geometry

É um tipo de problema genérico que pode ser colocado com outros tipos de problema. Por exemplo: círculo, elipse, parábola, inclinação.
Hyperbola

Problemas com hipérboles. Por exemplo: encontrar a interseção em x de (x^2)/4 - (y^2)/5 = 1.
Inflection Point

Encontrar o ponto de inflexão de f(x) = 1/2x^4 +x^3 - 6x^2.
Integral

Integral da raiz quadrada (x^2 - y^2).
Intercept

Problemas com interseções de linhas. Por exemplo: localizar a interseção em x da linha y = 10x - 5.
Limit

Problemas de limites. Por exemplo: encontrar o limite de x à medida que x se aproxima de 1 para (x^2-1)/(x-1).
Line Equation

Problemas de equação de linha. Por exemplo: encontrar a equação de uma linha com os pontos (-7,-4) e (-2,-6).
Linear Algebra

É um tipo de problema genérico que pode ser colocado com outros tipos de problema. Por exemplo: matrizes e polinômios característicos.
Linear Equation

Equações lineares. Por exemplo: 4x - 3 = 2x + 9.
Linear Inequality

Desigualdades lineares. Por exemplo: 5x - 6 > 3x - 8.
Logarithmic Equation

Equações logarítmicas. Por exemplo: log(x) = log(100).
Logarithmic Inequality

Desigualdades logarítmicas. Por exemplo: log(x) > log(100).
Matrix

Redução de linha {{1,2,5}, {3,-1,1}, {1,2,3}}
Midpoint

Problemas de ponto médio. Por exemplo: encontrar o ponto médio entre (-3, 7) e (5, -2).
Parabola

Problemas com parábolas. Por exemplo: encontrar o vértice de y2 - 4x - 4y = 0.
Parallel

Problemas com linhas paralelas. Por exemplo: verificar se duas linhas são paralelas (y = 10x + 5, y = 20x + 10).
Perpendicular

Problemas perpendiculares. Por exemplo: verificar se duas linhas são perpendiculares (y = 10x + 5, y = 20x + 10).
Polynomial Equation

Equações polinomiais. Por exemplo: x^5 - 3x = 0.
Polynomial Expression

Expressões polinomiais. Por exemplo: (x - 5)^4 * (x + 5)^2.
Polynomial Inequality

Desigualdades polinomiais. Por exemplo: x^4 - x^2 - 6 > x^3 - 3x^2.
Quadratic Equation

Equações quadráticas. Por exemplo: x^2 - 3x - 4 = 0.
Quadratic Expression

Expressões quadráticas. Por exemplo: x^2 - 3x - 2.
Quadratic Inequality

Desigualdades quadráticas. Por exemplo: x^2 - x - 6 > x^2 - 3x.
Radical Equation

Equações radicais. Por exemplo: sqrt(x) - x = 0.
Radical Inequality

Desigualdades radicais. Por exemplo: sqrt(x) - x > 0.
Rational Equation

Equações racionais. Por exemplo: 5/(x - 3) = 2/(x - 1).
Rational Expression

Expressões racionais. Por exemplo: 1/(x^3 + 4x^2 + 5x + 2).
Rational Inequality

Desigualdades racionais. Por exemplo: 5/(x - 3) > 2/(x - 1).
Slope

Problemas com inclinações. Por exemplo: encontrar a inclinação de y = 10x + 5.
Statistics

Problemas de estatísticas. Por exemplo: encontrar a média de um conjunto de números (3, 8, 2, 10).
System of Equations

Problemas de sistema de equações. Por exemplo: resolver 2x + 5y = 16;3x - 5y = - 1.
Trigonometry

Resolver sin(t) + cos(t) = 1.