Uporządkowane dane rozwiązań matematycznych (MathSolver)

Możesz pomóc uczniom, nauczycielom i innym osobom w rozwiązywaniu zadań matematycznych, dodając uporządkowane dane, które wskażą typ zadania matematycznego i przekierują do szczegółowych instrukcji jego rozwiązania. Oto przykład rozwiązania matematycznego w wynikach wyszukiwania Google (jego wygląd może ulec zmianie):

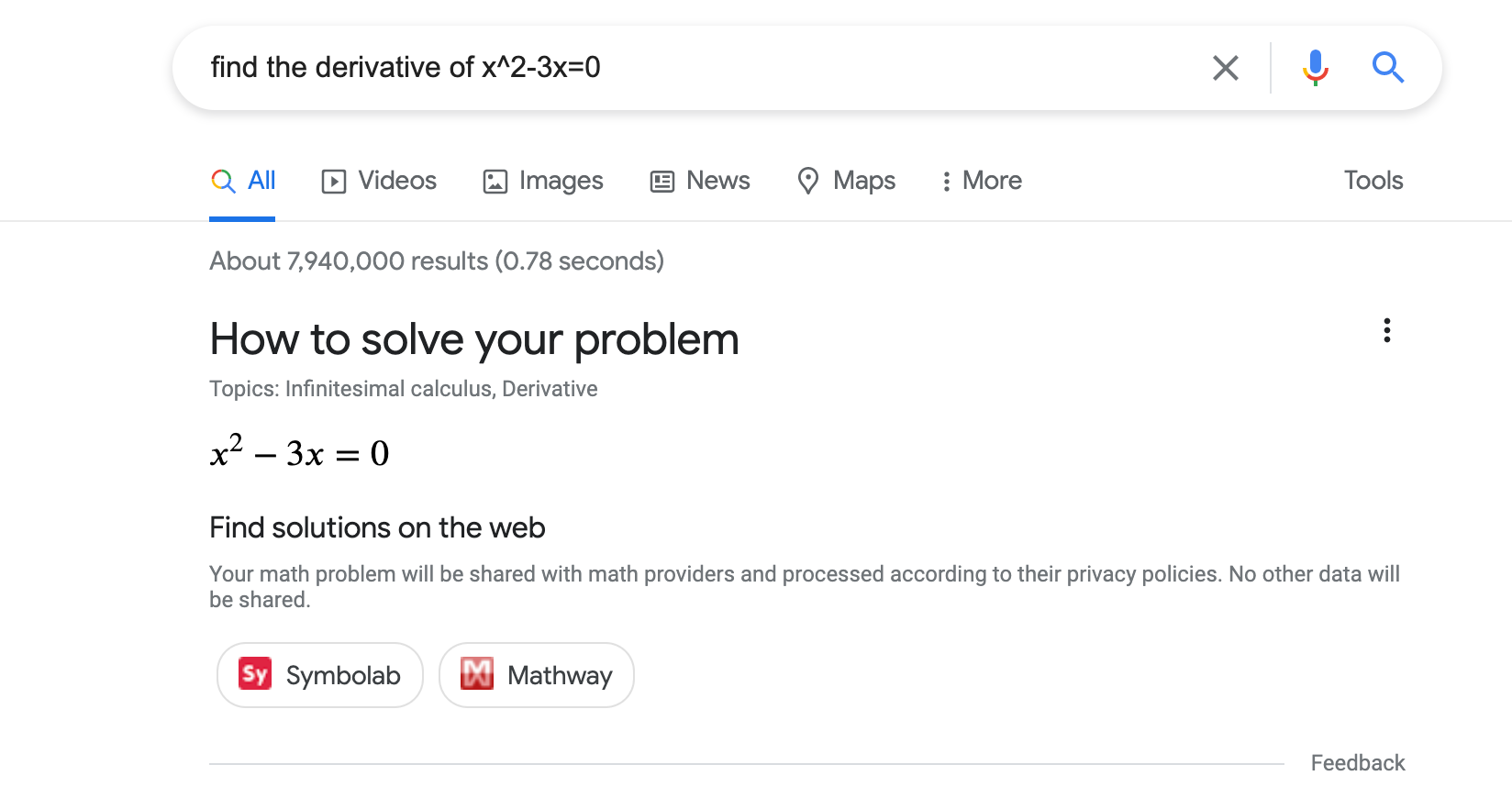
Przykład wyniku z elementami rozszerzonymi zawierającymi rozwiązanie matematyczne

Dodawanie uporządkowanych danych

Uporządkowane dane to standardowy format udostępniania informacji o stronie i klasyfikowania jej zawartości. Jeśli dopiero zaczynasz, dowiedz się, jak działają uporządkowane dane.

Poniżej omawiamy sposób tworzenia, testowania i udostępniania uporządkowanych danych. Szczegółowe instrukcje dodawania uporządkowanych danych do strony internetowej znajdziesz w ćwiczeniach z programowania poświęconych uporządkowanym danym.

  1. Dodaj wymagane właściwości. Dowiedz się, w którym miejscu na stronie umieścić uporządkowane dane w zależności od używanego formatu.
  2. Przestrzegaj wskazówek.
  3. Zweryfikuj kod za pomocą testu wyników z elementami rozszerzonymi i napraw błędy krytyczne. Rozważ też usunięcie niekrytycznych problemów, które mogą zostać zgłoszone w narzędziu – to może poprawić jakość uporządkowanych danych (ale nie jest to konieczne, aby witryna kwalifikowała się do wyników z elementami rozszerzonymi).
  4. Możesz wdrożyć kilka stron z uporządkowanymi danymi i dzięki narzędziu do sprawdzania adresów URL zobaczyć, jak Google je odczytuje. Upewnij się, że Twoja strona jest dostępna dla Google i nie jest blokowana przez plik robots.txt lub tag noindex ani nie wymaga logowania. Jeśli strona wygląda dobrze, możesz poprosić Google o ponowne zindeksowanie adresów URL.
  5. Aby na bieżąco informować Google o przyszłych zmianach, prześlij mapę witryny. Możesz zautomatyzować ten proces za pomocą interfejsu Search Console Sitemap API.

Przykłady

Rozwiązanie 1 problemu

Przykład dostępnej w języku angielskim i hiszpańskim strony głównej rozwiązania matematycznego z 1 działaniem, które może rozwiązać równania wielomianowe i zadania z pochodnymi.


<html>
<head>
<title>An awesome math solver</title>
</head>
<body>
<script type="application/ld+json">
[
  {
    "@context": "https://schema.org",
    "@type": ["MathSolver", "LearningResource"],
    "name": "An awesome math solver",
    "url": "https://www.mathdomain.com/",
    "usageInfo": "https://www.mathdomain.com/privacy",
    "inLanguage": "en",
    "potentialAction": [{
      "@type": "SolveMathAction",
      "target": "https://mathdomain.com/solve?q={math_expression_string}",
      "mathExpression-input": "required name=math_expression_string",
      "eduQuestionType": ["Polynomial Equation","Derivative"]
     }],
    "learningResourceType": "Math solver"
  },
  {
    "@context": "https://schema.org",
    "@type": ["MathSolver", "LearningResource"],
    "name": "Un solucionador de matemáticas increíble",
    "url": "https://es.mathdomain.com/",
    "usageInfo": "https://es.mathdomain.com/privacy",
    "inLanguage": "es",
    "potentialAction": [{
      "@type": "SolveMathAction",
      "target": "https://es.mathdomain.com/solve?q={math_expression_string}",
      "mathExpression-input": "required name=math_expression_string",
      "eduQuestionType": ["Polynomial Equation","Derivative"]
     }],
    "learningResourceType": "Math solver"
  }
]
</script>
</body>
</html>

Dwa działania rozwiązania

Przykład strony głównej rozwiązania matematycznego z 2 punktami końcowymi: jeden z nich może rozwiązywać równania wielomianowe, a drugi równania trygonometryczne. Strona jest dostępna tylko w języku angielskim.


<html>
<head>
<title>An awesome math solver</title>
</head>
<body>
<script type="application/ld+json">
{
  "@context": "https://schema.org",
  "@type": ["MathSolver", "LearningResource"],
  "name": "An awesome math solver",
  "url": "https://www.mathdomain.com/",
  "usageInfo": "https://www.mathdomain.com/privacy",
  "inLanguage": "en",
  "potentialAction": [{
     "@type": "SolveMathAction",
     "target": "https://mathdomain.com/solve?q={math_expression_string}",
     "mathExpression-input": "required name=math_expression_string",
     "eduQuestionType": "Polynomial Equation"
   },
   {
     "@type": "SolveMathAction",
     "target": "https://mathdomain.com/trig?q={math_expression_string}",
     "mathExpression-input": "required name=math_expression_string",
     "eduQuestionType": "Trigonometric Equation"
   }],
  "learningResourceType": "Math solver"
}
</script>
</body>
</html>

Wytyczne

Aby Twoja strona mogła wyświetlać się w wynikach z elementami rozszerzonymi zawierającymi rozwiązania matematyczne, musisz przestrzegać tych wytycznych:

Wskazówki techniczne

  • Dodaj do strony głównej witryny uporządkowane dane MathSolver.
  • Upewnij się, że Googlebot może wydajnie indeksować Twoją witrynę.
  • Jeśli masz kilka identycznych kopii tego samego rozwiązania matematycznego hostowanych pod różnymi adresami URL, używaj kanonicznych adresów URL na każdej kopii strony.
  • Nie zezwalamy na rozwiązania matematyczne, które są dostępne tylko po zalogowaniu się lub w sekcji płatnej. Rozwiązanie i szczegółowe omówienie początkowego zadania muszą być dostępne dla użytkowników, którzy trafiają do Twojej witryny przez tę funkcję w Google. Dodatkowe treści mogą być widoczne po zalogowaniu się lub w sekcji płatnej.

Wskazówki dotyczące treści

Opracowaliśmy te wskazówki dotyczące rozwiązań matematycznych, aby mieć pewność, że użytkownicy mają dostęp do odpowiednich zasobów edukacyjnych. Jeśli znajdziemy treści, które naruszają te zasady, odpowiednio zareagujemy, co może skutkować m.in. podjęciem ręcznego działania i usunięciem Twoich stron z interfejsu rozwiązań matematycznych w Google.

  • Nie zezwalamy na treści promocyjne udające rozwiązania matematyczne, takie jak treści publikowane przez inne firmy (np. dotyczące programów partnerskich).
  • Odpowiadasz za dokładność i jakość rozwiązań matematycznych w tej funkcji. Jeśli w ramach naszych procesów sprawdzania jakości okaże się, że Twoje dane są niedokładne, możemy usunąć z funkcji Twoje rozwiązanie, dopóki nie poprawisz błędów (w zależności od ich wagi). Dotyczy to:
    • dokładności typów rozwiązywanych zadań,
    • deklarowanej dokładności rozwiązań.

Definicje typów uporządkowanych danych

Aby treści mogły wyświetlać się w wynikach z elementami rozszerzonymi, musisz w nich zastosować wymagane właściwości. Możesz też dodać do nich właściwości zalecane, by wzbogacić informacje podane w uporządkowanych danych i zwiększyć w ten sposób wygodę użytkowników.

MathSolver

MathSolver to narzędzie, które pomaga uczniom, nauczycielom i innym osobom w zadaniach matematycznych, wyświetlając szczegółowe rozwiązania. Używaj uporządkowanych danych MathSolver na stronie głównej witryny.

Pełną definicję znaczników MathSolver znajdziesz na schema.org/MathSolver.

Właściwości obsługiwane przez Google:

Właściwości wymagane
potentialAction

SolveMathAction

Działanie, które prowadzi do podania wyjaśnienia (np. może to być szczegółowe rozwiązanie lub wykres) wyrażenia matematycznego.

{
"@type": "MathSolver",
"potentialAction": [{
  "@type": "SolveMathAction",
  "target": "https://mathdomain.com/solve?q={math_expression_string}",
  "mathExpression-input": "required name=math_expression_string",
  "eduQuestionType": "Polynomial Equation"
  }]
}
potentialAction.mathExpression-input

Text

Obiekt zastępczy wyrażenia matematycznego (np. x^2-3x=0), który jest wysyłany przez Google do Twojej witryny. Następnie możesz „rozwiązać” wyrażenie matematyczne, co może obejmować uproszczenie, przekształcenie lub rozwiązanie konkretnej zmiennej. Ciąg może mieć wiele formatów (np: LaTeX, Ascii-Math lub wyrażenie matematyczne, które można wpisać na klawiaturze).

W przypadku niektórych typów problemów właściwość math_expression_string wskazuje zarówno typ problemu, jak i jego parametry. Oto przykłady bardziej złożonych typów problemów, które można poprawnie przewidzieć i przeanalizować.

Instrumenty pochodne

Google wysyła math_expression_string na jeden z tych 2 sposobów:

  • (math_expression)'
  • d/dvariable math_expression

Examples:

  • (x^2+x)'
  • d/dx (x^2+x)
  • d/dy y^2+y

Integrals

Google will send a math_expression_string in one of two forms:

  • \int math_expression
  • \int_{from}^{to} math_expression

Przykłady:

  • \int x^2+x
  • \int_{0}^{2} x^2+x

Limity

Google wysyła math_expression_string na jeden z tych 2 sposobów:

  • \lim math_expression
  • \lim_{variable\rightarrowvalue} math_expression

Przykłady:

  • \lim_{x\rightarrow0} sin(x)/x
  • \lim_{y\rightarrow\infty} sin(y)/y
  • \lim sin(x)/x
url

URL

Adres URL MathSolver.
usageInfo

URL

Polityka prywatności witryny z rozwiązaniami zagadnień matematycznych.

{
  "@type": "MathSolver",
  "usageInfo": "https://www.mathdomain.com/privacy"
}
potentialAction.target

EntryPoint

Adres URL punktu wejścia dla działania. Właściwość potentialAction.target akceptuje ciąg, który reprezentuje wyrażenie matematyczne będące przedmiotem działania.

{
"@type": "MathSolver",
"potentialAction": [{
  "@type": "SolveMathAction",
  "target": "https://mathdomain.com/solve?q={math_expression_string}"
  }]
}
Właściwości zalecane
inLanguage

Text

Języki, w których działa Twoja witryna z rozwiązaniami zagadnień matematycznych. Listę dostępnych języków znajdziesz w tej tabeli.

{
  "@type": "MathSolver",
  "inLanguage": "es"
}
assesses

Lista Text definicji typów zadań

Typy zadań, które rozwiązuje HowTo. Używaj właściwości assesses, jeśli używasz znaczników HowTo oprócz znaczników MathSolver.

{
  "@type": "MathSolver",
  "assesses": "Polynomial Equation"
}
potentialAction.eduQuestionType

Lista Text definicji typów zadań

Typy zadań, które można rozwiązać przy użyciu właściwości potentialAction.target.

{
  "@type": "SolveMathAction",
  "eduQuestionType": "Polynomial Equation"
}

LearningResource

LearningResource wskazuje, że przedmiotem znaczników jest zasób, który pomaga uczniom, nauczycielom i innym osobom w nauce. Używaj LearningResource na stronie głównej witryny.

Pełną definicję znaczników LearningResource znajdziesz na schema.org/LearningResource.

Właściwości obsługiwane przez Google:

Właściwości wymagane
learningResourceType

Text

Typ zasobu edukacyjnego. Używaj tej stałej wartości: Math Solver.

{
  "@type": ["MathSolver", "LearningResource"],
  "learningResourceType": "Math Solver"
}

Definicje typów zadań

Używaj listy typów zadań jako właściwości eduQuestionType dla MathSolver.potentialAction lub dla pola assesses w uporządkowanych danych MathSolver, gdy MathSolver towarzyszy uporządkowanym danym HowTo, które wskazują szczegółowe instrukcje rozwiązania zadania.

W tabeli poniżej znajdziesz przykłady typów zadań, do których możesz dodać adnotacje:

Przykładowe typy zadań (nie jest to kompletna lista)
Absolute Value Equation

Równania z wartością bezwzględną. Przykład: |x – 5| = 9
Algebra

Typ zadań ogólnych, które można umieszczać razem z innymi typami zadań. Na przykład: równania wielomianowe, równania wykładnicze i równania pierwiastkowe.
Arc Length

Zadania z długością krzywej. Na przykład: określ długość x = 4 (3 + y)^2, 1 < y < 4.
Arithmetic

Zadania arytmetyczne. Na przykład: znajdź sumę 5 + 7.
Biquadratic Equation

Równania dwukwadratowe. Na przykład: x^4 – x^2 – 2 = 0.
Calculus

Typ zadań ogólnych, które można umieszczać razem z innymi typami zadań. Na przykład: całki, pochodne i równania różniczkowe.
Characteristic Polynomial

Znajdź wielomian charakterystyczny {{1,2,5}, {3,-1,1}, {1,2,3}}.
Circle

Zadania związane z okręgami. Na przykład: znajdź promień x^2 + y^2 = 3.
Derivative

Pochodna 5x^4 + 2x^3 + 4x – 2.
Differential Equation

Zadania z równaniami różniczkowymi. Na przykład: y + dy/dx=5x.
Distance

Zadania z obliczaniem odległości. Na przykład: znajdź odległość między (6,-1) i (-3,2).
Eigenvalue

Zadania z wartością własną. Na przykład: znajdź wartości własne macierzy [[-6, 3], [4, 5]].
Eigenvector

Zadania z wektorem własnym. Na przykład: znajdź wektor własny macierzy [[-6, 3], [4, 5]] z wartościami własnymi [-7, 6].
Ellipse

Zadania z elipsami. Na przykład: znajdź punkty przecięcia z osiami x i y w równaniu 9x^2 + 4y^2 = 36.
Exponential Equation

Równania wykładnicze. Na przykład: 7^x = 9.
Function

Uproszczenia wielomianów. Na przykład: (x-5)^2 * (x+5)^2.
Function Composition

f(g(x)) gdy f(x) = x^2 – 2x, g(x) = 2x – 2
Geometry

Typ zadań ogólnych, które można umieszczać razem z innymi typami zadań. Na przykład: okrąg, elipsa, parabola, nachylenie.
Hyperbola

Zadania z hiperbolą. Na przykład: znajdź punkt przecięcia z osią x dla równania (x^2)/4 – (y^2)/5 = 1.
Inflection Point

Znajdź punkt przegięcia f(x) = 1/2 x 4 + x ^ 3 – 6 x ^ 2.
Integral

Całka z pierwiastka kwadratowego (x^2 – y^2).
Intercept

Zadania z punktami przecięcia prostej. Na przykład: znajdź punkt przecięcia prostej z osią x, gdy y = 10x – 5.
Limit

Zadania z granicą. Na przykład: znajdź granicę x, gdy x zbliża się do 1 dla (x^2 – 1)/(x – 1).
Line Equation

Zadania z równaniem prostej. Na przykład: znajdź równanie prostej z punktami (-7, -4) i (-2, -6).
Linear Algebra

Typ zadań ogólnych, które można umieszczać razem z innymi typami zadań. Na przykład: macierz i wielomian charakterystyczny.
Linear Equation

Równania liniowe. Na przykład: 4x – 3 = 2x + 9.
Linear Inequality

Nierówności liniowe. Na przykład: 5x – 6 > 3x – 8.
Logarithmic Equation

Równania logarytmiczne. Na przykład: log(x) = log(100).
Logarithmic Inequality

Nierówności logarytmiczne. Na przykład: log(x) > log(100).
Matrix

{{1,2,5}, {3,-1,1}, {1,2,3}} postać schodkowa
Midpoint

Zadania z punktem środkowym. Na przykład: znajdź punkt środkowy między (-3, 7) a (5, -2).
Parabola

Zadania z parabolą. Na przykład: znajdź wierzchołek y2 – 4x – 4y = 0.
Parallel

Zadania z prostymi równoległymi. Na przykład: czy te 2 proste są równoległe (y = 10x + 5, y = 20x + 10)?
Perpendicular

Zadania z prostopadłymi. Na przykład: czy te 2 proste są prostopadłe (y = 10x + 5, y = 20x + 10)?
Polynomial Equation

Równania wielomianowe. Na przykład: x^5 – 3x = 0.
Polynomial Expression

Wyrażenia wielomianowe. Na przykład: (x – 5)^4 * (x + 5)^2.
Polynomial Inequality

Nierówności wielomianowe. Na przykład: x^4 – x^2 – 6 > x^3 – 3x^2.
Quadratic Equation

Równania kwadratowe. Na przykład: x^2 – 3x – 4 = 0.
Quadratic Expression

Wyrażenia kwadratowe. Na przykład: x^2 – 3x – 2.
Quadratic Inequality

Nierówności kwadratowe. Na przykład: x^2 – x – 6 > x^2 – 3x.
Radical Equation

Równania pierwiastkowe. Na przykład: sqrt(x) – x = 0.
Radical Inequality

Nierówności pierwiastkowe. Na przykład: sqrt(x) – x > 0.
Rational Equation

Równania wymierne. Na przykład: 5/(x – 3) = 2/(x – 1).
Rational Expression

Wyrażenia wymierne. Na przykład: 1/(x^3 + 4x^2 + 5x + 2).
Rational Inequality

Nierówności wymierne. Na przykład: 5/(x – 3) > 2/(x – 1).
Slope

Obliczanie nachylenia. Na przykład: znajdź nachylenie prostej y = 10x + 5.
Statistics

Zadania statystyczne. Na przykład: znajdź średnią dla zbioru liczb (3, 8, 2, 10).
System of Equations

Zadania z układami równań. Na przykład: rozwiąż układ równań: 2x + 5y = 16; 3x – 5y = –1.
Trigonometry

Znajdź sin(t) + cos(t) = 1.