البيانات المنظَّمة لأداة حلّ المسائل الرياضية (MathSolver)

لمساعدة الطلاب والمعلمين والمستخدمين الآخرين في حل المسائل الرياضية، يمكنك استخدام البيانات المنظَّمة للإشارة إلى نوع المسألة الرياضية وإدراج روابط تؤدي إلى التعليمات المفصّلة لحلّ مسائل محدّدة. في ما يلي مثال على الشكل الذي قد تظهر به أدوات حلّ المسائل الرياضية في نتائج البحث على Google (يجوز أن يتغيّر المظهر):

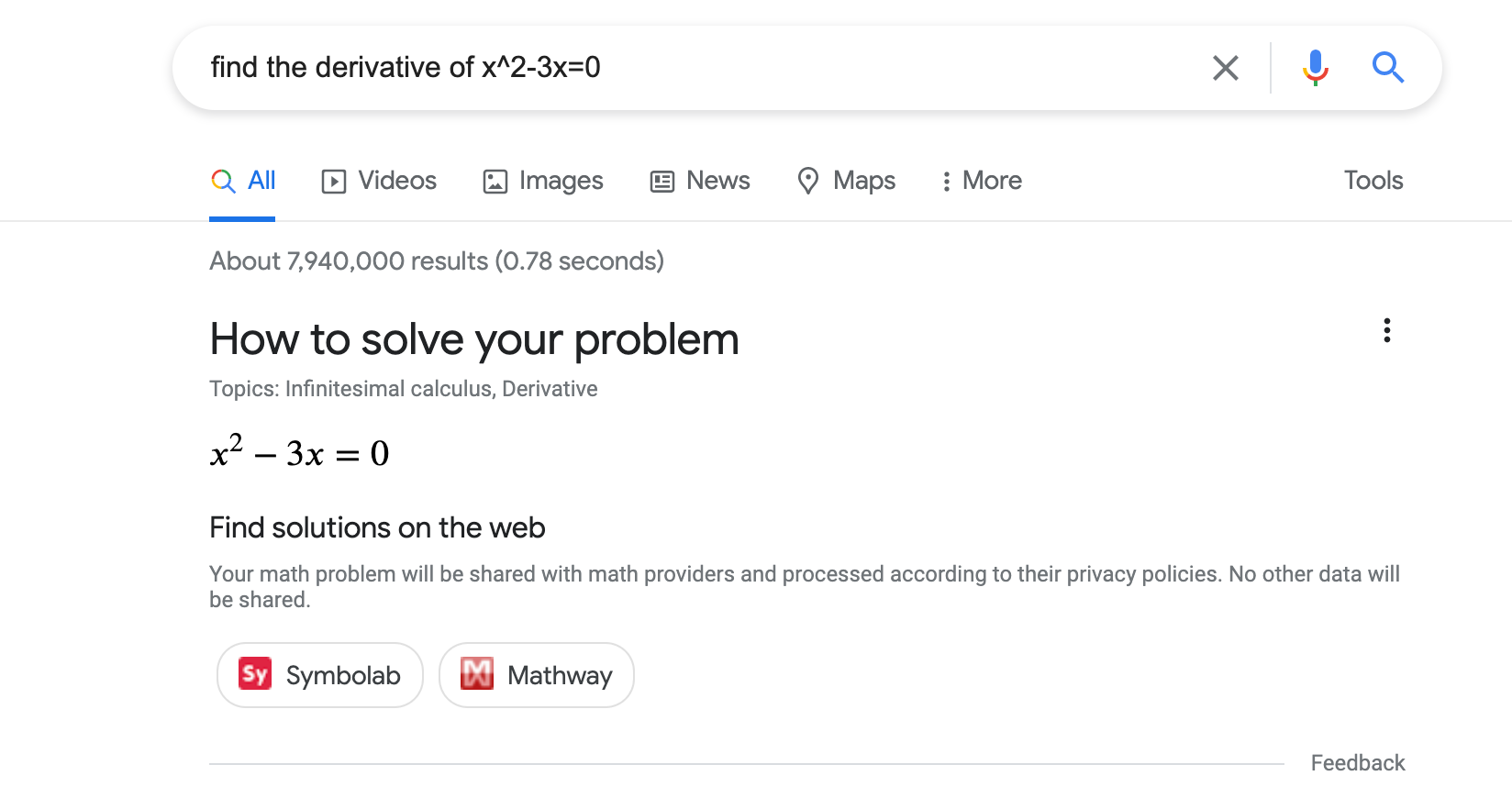
مثال على نتيجة غنية بصريًا لأدوات حلّ المسائل الرياضية

كيفية إضافة البيانات المنظَّمة

البيانات المنظَّمة هي تنسيق موحّد لتقديم معلومات عن صفحة محدّدة وتصنيف محتواها. إذا كنت لا تزال مبتدئًا في مجال البيانات المنظَّمة، يمكنك الاطّلاع على المزيد من المعلومات حول آلية عمل البيانات المنظَّمة.

إليك نظرة عامة حول كيفية إنشاء بيانات منظَّمة واختبارها وإصدارها.

  1. أضِف السمات المطلوبة. استنادًا إلى التنسيق الذي تستخدمه، يمكنك معرفة مكان إدراج البيانات المنظَّمة في الصفحة.
  2. اتّبِع الإرشادات.
  3. تحقَّق من صحة الرمز باستخدام اختبار النتائج الغنية بصريًا، وأصلِح أي أخطاء ملحّة. ننصحك أيضًا بحلّ أي مشاكل غير ملحّة قد ترصدها الأداة لأنّ ذلك قد يساعدك على تحسين جودة بياناتك المنظَّمة (ولكن هذا الإجراء ليس ضروريًا لتكون بياناتك مؤهّلة للظهور ضمن النتائج الغنية بصريًا).
  4. انشر بعض الصفحات التي تتضمّن بياناتك المنظَّمة واستخدِم أداة فحص عنوان URL لاختبار الطريقة التي يرى بها محرّك بحث Google الصفحة. تأكَّد من إمكانية وصول محرّك بحث Google إلى صفحتك ومن عدم حظرها باستخدام ملف robots.txt أو علامة noindex أو متطلبات تسجيل الدخول. إذا بدت الصفحة جيدة، يمكنك أن تطلب من محرّك بحث Google إعادة الزحف إلى عناوين URL الخاصة بك.
  5. لإعلام محرّك بحث Google بأي تغييرات لاحقة، ننصحك بإرسال خريطة الموقع. يمكنك برمجة هذا الإجراء باستخدام Search Console Sitemap API.

أمثلة

إجراء واحد للحل

في ما يلي مثال على صفحة رئيسية لأداة حل المسائل الرياضية تتضمّن إجراءً واحدًا للحلّ يمكنه حلّ المعادلات المتعددة الحدود ومسائل المشتقات، وتتوفّر باللغتين الإنجليزية والإسبانية.


<html>
<head>
<title>An awesome math solver</title>
</head>
<body>
<script type="application/ld+json">
[
  {
    "@context": "https://schema.org",
    "@type": ["MathSolver", "LearningResource"],
    "name": "An awesome math solver",
    "url": "https://www.mathdomain.com/",
    "usageInfo": "https://www.mathdomain.com/privacy",
    "inLanguage": "en",
    "potentialAction": [{
      "@type": "SolveMathAction",
      "target": "https://mathdomain.com/solve?q={math_expression_string}",
      "mathExpression-input": "required name=math_expression_string",
      "eduQuestionType": ["Polynomial Equation","Derivative"]
     }],
    "learningResourceType": "Math solver"
  },
  {
    "@context": "https://schema.org",
    "@type": ["MathSolver", "LearningResource"],
    "name": "Un solucionador de matemáticas increíble",
    "url": "https://es.mathdomain.com/",
    "usageInfo": "https://es.mathdomain.com/privacy",
    "inLanguage": "es",
    "potentialAction": [{
      "@type": "SolveMathAction",
      "target": "https://es.mathdomain.com/solve?q={math_expression_string}",
      "mathExpression-input": "required name=math_expression_string",
      "eduQuestionType": ["Polynomial Equation","Derivative"]
     }],
    "learningResourceType": "Math solver"
  }
]
</script>
</body>
</html>

إجراءان للحلّ

في ما يلي مثال على صفحة رئيسية تتضمّن نقطتَي نهاية للحلّ: نقطة نهاية لحل المعادلات المتعددة الحدود ونقطة نهاية أخرى لحلّ معادلات حساب المثلثات. لا يتوفّر هذا الترميز إلا باللغة الإنجليزية.


<html>
<head>
<title>An awesome math solver</title>
</head>
<body>
<script type="application/ld+json">
{
  "@context": "https://schema.org",
  "@type": ["MathSolver", "LearningResource"],
  "name": "An awesome math solver",
  "url": "https://www.mathdomain.com/",
  "usageInfo": "https://www.mathdomain.com/privacy",
  "inLanguage": "en",
  "potentialAction": [{
     "@type": "SolveMathAction",
     "target": "https://mathdomain.com/solve?q={math_expression_string}",
     "mathExpression-input": "required name=math_expression_string",
     "eduQuestionType": "Polynomial Equation"
   },
   {
     "@type": "SolveMathAction",
     "target": "https://mathdomain.com/trig?q={math_expression_string}",
     "mathExpression-input": "required name=math_expression_string",
     "eduQuestionType": "Trigonometric Equation"
   }],
  "learningResourceType": "Math solver"
}
</script>
</body>
</html>

الإرشادات

يجب اتّباع الإرشادات التالية لتكون صفحتك مؤهّلة للعرض في النتائج الغنية بصريًا لأدوات حل المسائل الحسابية:

الإرشادات الفنية

  • أضِف بيانات MathSolver المنظَّمة إلى الصفحة الرئيسية في موقعك الإلكتروني.
  • تأكَّد من أنّ بإمكان Googlebot الزحف إلى موقعك الإلكتروني بفعالية.
  • إذا كان لديك عدة نُسخ متطابقة من أداة حلّ المسائل الرياضية نفسها تتم استضافتها ضمن عناوين URL مختلفة، استخدِم عناوين URL الأساسية في كل نسخة من الصفحة.
  • لا نسمح بأدوات حلّ المسائل الرياضية التي يتم إخفاؤها تمامًا خلف معلومات تسجيل الدخول أو جدار الدفع. بعد انتقال المستخدمين من الميزة على Google إلى موقعك الإلكتروني، يجب أن يتمكّنوا من الوصول بسهولة إلى الحلّ والاطّلاع على التعليمات المفصّلة لحلّ مسألتهم الأساسية. ويمكن إخفاء المحتوى الإضافي خلف معلومات تسجيل الدخول أو جدار الدفع.

إرشادات المحتوى

لقد وضعنا إرشادات المحتوى هذه الخاصة بأدوات حلّ المسائل الرياضية لضمان وصول المستخدمين إلى الموارد التعليمية ذات الصلة. وإذا اكتشفنا محتوى يخالف هذه السياسات، سنستجيب بشكل مناسب، ما قد يتضمّن اتّخاذ إجراء يدوي ومنع صفحاتك من الظهور في تجربة أداة حلّ المسائل الرياضية على Google.

  • لا نسمح بنشر المحتوى الترويجي المتخفّي في شكل أداة لحلّ المسائل الرياضية، مثل المحتوى الذي تنشره جهة خارجية (على سبيل المثال، برامج الشركاء التابعين).
  • تقع على عاتقك مسؤولية ضمان دقة وجودة أداة حلّ المسائل الرياضية المعروضة من خلال هذه الميزة. وإذا تبيّن أنّ قدرًا معيّنًا من بياناتك غير دقيق استنادًا إلى عمليات المراجعة التي نجريها للجودة، قد تتم إزالة أداة الحلّ الخاصة بك من الميزة إلى أن تحلّ المشاكل بناءً على درجة الخطورة. ينطبق هذا الأمر على:
    • دقة أنواع المسائل التي يمكن للأداة حلّها
    • دقة الحلول للمسائل الرياضية التي تؤكّد الأداة إمكانية حلّها

تعريفات أنواع البيانات المنظَّمة

يجب تضمين السمات المطلوبة لكي يصبح المحتوى مؤهّلاً للعرض كنتيجة غنيّة بصريًا. يمكنك أيضًا تضمين السمات المقترَحة لإضافة مزيد من المعلومات إلى بياناتك المنظَّمة، ما يؤدي إلى تحسين التجربة التي تقدمها للمستخدم.

MathSolver

‫MathSolver هي أداة تساعد الطلاب والمعلّمين والمستخدمين الآخرين في حلّ المسائل الرياضية من خلال وضع حلول مفصّلة. استخدِم بيانات MathSolver المنظَّمة في الصفحة الرئيسية على موقعك الإلكتروني.

يتوفّر التعريف الكامل للسمة MathSolver على schema.org/MathSolver.

في ما يلي السمات المتوافقة مع Google:

السمات المطلوبة
potentialAction

SolveMathAction

تمثّل هذه السمة الإجراء الذي يؤدي إلى تفسير رياضي (على سبيل المثال، حلّ مفصّل أو رسم بياني) لتعبير حسابي.

{
"@type": "MathSolver",
"potentialAction": [{
  "@type": "SolveMathAction",
  "target": "https://mathdomain.com/solve?q={math_expression_string}",
  "mathExpression-input": "required name=math_expression_string",
  "eduQuestionType": "Polynomial Equation"
  }]
}
potentialAction.mathExpression-input

Text

تمثّل هذه السمة عنصرًا نائبًا لتعبير حسابي (على سبيل المثال: x^2-3x=0) يرسله محرّك بحث Google إلى موقعك الإلكتروني. ويمكنك عند ذلك "حلّ" التعبير الحسابي، الذي يمكن حلّه لمتغير محدد أو تبسيطه أو تحويله. وقد تكون هذه السلسلة بتنسيقات متعدّدة (على سبيل المثال: LaTeX أو Ascii-Math أو التعبيرات الحسابية التي يمكنك كتابتها باستخدام لوحة المفاتيح).

بالنسبة إلى بعض أنواع المسائل الحسابية، تشير السمة math_expression_string إلى كل من نوع المسألة ومَعلمات نوع المسألة. في ما يلي بعض الأمثلة على أنواع المسائل الحسابية الأكثر تعقيدًا لتتمكّن من توقّعها وتحليلها بشكل صحيح.

المشتقات

سيرسل Google القيمة math_expression_string بأحد التنسيقَين التاليَين:

  • (math_expression)'
  • d/dvariable math_expression

Examples:

  • (x^2+x)'
  • d/dx (x^2+x)
  • d/dy y^2+y

Integrals

Google will send a math_expression_string in one of two forms:

  • \int math_expression
  • \int_{from}^{to} math_expression

أمثلة:

  • \int x^2+x
  • \int_{0}^{2} x^2+x

النهايات

سيرسل Google القيمة math_expression_string بأحد التنسيقَين التاليَين:

  • \lim math_expression
  • \lim_{variable\rightarrowvalue} math_expression

أمثلة:

  • \lim_{x\rightarrow0} sin(x)/x
  • \lim_{y\rightarrow\infty} sin(y)/y
  • \lim sin(x)/x
url

URL

تمثّل هذه السمة عنوان URL الخاص بالسمة MathSolver.
usageInfo

URL

تمثّل هذه السمة سياسة الخصوصية المتّبعة على موقعك الإلكتروني الخاص بحل المسائل الحسابية.

{
  "@type": "MathSolver",
  "usageInfo": "https://www.mathdomain.com/privacy"
}
potentialAction.target

EntryPoint

تمثّل هذه السمة نقطة إدخال عنوان URL الهدف لأحد الإجراءات. وتقبل السمة potentialAction.target سلسلة لتمثيل التعبير الحسابي الذي يتم حلّه عن طريق الإجراء.

{
"@type": "MathSolver",
"potentialAction": [{
  "@type": "SolveMathAction",
  "target": "https://mathdomain.com/solve?q={math_expression_string}"
  }]
}
السمات المقترَحة
inLanguage

Text

تمثّل هذه السمة اللغات المتاحة على الموقع الإلكتروني الخاص بحلّ المسائل الرياضية. انتقِل إلى هذا الجدول للاطّلاع على قائمة باللغات المحتملة.

{
  "@type": "MathSolver",
  "inLanguage": "es"
}
assesses

Text قائمة تعريفات أنواع المسائل

تمثّل هذه السمة أنواع المسائل التي يتم حلّها باستخدام HowTo. استخدِم السمة assesses إذا كنت تستخدم ترميز HowTo بالإضافة إلى ترميز MathSolver.

{
  "@type": "MathSolver",
  "assesses": "Polynomial Equation"
}
potentialAction.eduQuestionType

Text قائمة تعريفات أنواع المسائل

تمثّل هذه السمة أنواع المسائل التي يمكن حلّها باستخدام السمة potentialAction.target.

{
  "@type": "SolveMathAction",
  "eduQuestionType": "Polynomial Equation"
}

LearningResource

تشير السمة LearningResource إلى أنّ موضوع الترميز هو مورد يساعد الطلاب والمعلمين وغيرهم من المستخدمين في التعلّم الدراسي. استخدِم LearningResource على الصفحة الرئيسية في موقعك الإلكتروني.

يتوفّر التعريف الكامل للسمة LearningResource على schema.org/LearningResource.

في ما يلي السمات المتوافقة مع Google:

السمات المطلوبة
learningResourceType

Text

تمثّل هذه السمة نوع هذا المورد التعليمي. ويجب استخدام هذه القيمة الثابتة: Math Solver.

{
  "@type": ["MathSolver", "LearningResource"],
  "learningResourceType": "Math Solver"
}

تعريفات أنواع المسائل الحسابية

استخدِم القائمة التالية لأنواع المسائل الحسابية باعتبارها eduQuestionType للسمة MathSolver.potentialAction أو للحقل assesses في MathSolver عند مرافقة MathSolver للسمة HowTo التي تقدّم تعليمات بخصوص مسألة حسابية معيّنة.

يعرض الجدول التالي بعض الأمثلة لأنواع المسائل التي يمكنك إضافة تعليق توضيحي إليها:

أمثلة على المسائل الحسابية (هذه القائمة ليست شاملة)
Absolute Value Equation

تمثّل هذه السمة معادلات القيمة المطلقة. على سبيل المثال: ‎|x - 5| = 9
Algebra

تمثّل هذه السمة نوعًا عامًا من المسائل يمكن وضعه مع أنواع أخرى. على سبيل المثال: المعادلات المتعددة الحدود والمعادلات الأسية والتعبيرات الجذرية
Arc Length

تمثّل هذه السمة مسائل طول القوس. على سبيل المثال: حدِّد طول x = 4 (3 + y)^2, 1 < y < 4.
Arithmetic

مسائل رياضية على سبيل المثال: أوجِد مجموع 5 + 7.
Biquadratic Equation

تمثّل هذه السمة المعادلات الثنائية التربيع. على سبيل المثال: x^4 - x^2 - 2 = 0
Calculus

تمثّل هذه السمة نوعًا عامًا من المسائل يمكن وضعه مع أنواع أخرى. على سبيل المثال: التكامل والمشتقات والمعادلات التفاضلية
Characteristic Polynomial

أوجِد متعددة الحدود المميزة لـ {{1,2,5}, {3,-1,1}, {1,2,3}}.
Circle

تمثّل هذه السمة المسائل المتعلقة بالدوائر. على سبيل المثال: أوجِد نصف قطر x^2 + y^2 = 3.
Derivative

أوجِد مشتق 5x^4 + 2x^3 + 4x - 2.
Differential Equation

تمثّل هذه السمة مسائل المعادلات التفاضلية. على سبيل المثال: y+dy/dx=5x
Distance

تمثّل هذه السمة مسائل المسافة. على سبيل المثال: أوجِد المسافة بين ‎(6,-1) و‎(-3,2)
Eigenvalue

مسائل القيَم الذاتية على سبيل المثال: أوجِد القيَم الذاتية للمصفوفة [[-6، 3]، [4، 5]].
Eigenvector

مسائل المتّجِه الذاتي على سبيل المثال: أوجِد المتّجِه الذاتي للمصفوفة [[-6، 3]، [4، 5]] مع القيَم الذاتية لـ [-7، 6].
Ellipse

تمثّل هذه السمة المسائل المرتبطة بالقطع الناقص. على سبيل المثال، احسب نقطتَي التقاطع مع الأس السيني والأس الصادي في المعادلة 9x^2 + 4y^2 = 36.
Exponential Equation

تمثّل هذه السمة معادلات الدالة الأسية. على سبيل المثال: 7‎^x = 9
Function

تمثّل هذه السمة التبسيطات المتعددة الحدود. على سبيل المثال: ‎(x-5)^2 * (x+5)^2
Function Composition

f(g(x)) إذا كان f(x)=x^2-2x, g(x)=2x-2
Geometry

تمثّل هذه السمة نوعًا عامًا من المسائل يمكن وضعه مع أنواع أخرى. على سبيل المثال: الدائرة والقطع الناقص والقطع المكافئ والميل
Hyperbola

تمثّل هذه السمة مسائل القطع الزائد. على سبيل المثال: أوجِد نقطة التقاطع مع الأس السيني في المعادلة x (x^2)/4 - (y^2)/5 = 1
Inflection Point

أوجِد نقطة الانعطاف في المعادلة f(x) = 1/2x^4 + x^3 - 6x^2
Integral

تكامل الجذر التربيعي (x^2 - y^2)
Intercept

تمثّل هذه السمة مسائل تقاطع الخطوط. على سبيل المثال: أوجِد نقطة تقاطع الخط y = 10x - 5 مع الأس السيني.
Limit

مسائل النهاية على سبيل المثال: أوجِد نهاية x عندما يقترب x من 1 في المعادلة (x^2-1)/(x-1).
Line Equation

تمثّل هذه السمة مسائل معادلات الخط المستقيم. على سبيل المثال: أوجِد معادلة الخط الذي يمر بالنقطتين ‎(-7,-4) و‎(-2,-6).
Linear Algebra

تمثّل هذه السمة نوعًا عامًا من المسائل يمكن وضعه مع أنواع أخرى. على سبيل المثال: المصفوفة ومتعددة الحدود المميزة
Linear Equation

تمثّل هذه السمة المعادلات الخطية. على سبيل المثال: 4x - 3 = 2x + 9
Linear Inequality

تمثّل هذه السمة المتباينات الخطية. على سبيل المثال: 5x - 6 > 3x - 8
Logarithmic Equation

تمثّل هذه السمة المعادلات اللوغاريتمية. على سبيل المثال: log(x) = log(100)
Logarithmic Inequality

تمثّل هذه السمة المتباينات اللوغاريتمية. على سبيل المثال: log(x) > log(100)
Matrix

الاختزال صفيًا بمقدار {{1,2,5}, {3,-1,1}, {1,2,3}}
Midpoint

تمثّل هذه السمة المسائل حول نقطة المنتصف. على سبيل المثال: أوجِد نقطة المنتصف ما بين ‎(-3, 7) و‎(5, -2).
Parabola

تمثّل هذه السمة مسائل القطع المكافئ. على سبيل المثال: أوجِد الرأس في y2 - 4x - 4y = 0.
Parallel

تمثّل هذه السمة مسائل الخطوط المتوازية. على سبيل المثال: هل الخطان (y=10x + 5 و‎y + 20x + 10) متوازيان؟
Perpendicular

تمثّل هذه السمة مسائل التعامد. على سبيل المثال: هل الخطان (y=10x + 5 وy + 20x + 10) متعامدان؟
Polynomial Equation

تمثّل هذه السمة المعادلات المتعددة الحدود. على سبيل المثال: x^5 - 3x = 0
Polynomial Expression

تمثّل هذه السمة التعبيرات المتعددة الحدود. على سبيل المثال: ‎(x - 5)^4 * (x + 5)^2
Polynomial Inequality

تمثّل هذه السمة المتباينات المتعددة الحدود. على سبيل المثال: x^4 - x^2 - 6 > x^3 - 3x^2
Quadratic Equation

تمثّل هذه السمة المعادلات التربيعية. على سبيل المثال: x^2 - 3x - 4 = 0
Quadratic Expression

تمثّل هذه السمة التعبيرات التربيعية. على سبيل المثال: x^2 - 3x - 2
Quadratic Inequality

تمثّل هذه السمة المتباينات التربيعية. على سبيل المثال: x^2 - x - 6 > x^2 - 3x
Radical Equation

تمثّل هذه السمة المعادلات الجذرية. على سبيل المثال: sqrt(x) - x = 0
Radical Inequality

تمثّل هذه السمة المتباينات الجذرية. على سبيل المثال: sqrt(x) - x > 0
Rational Equation

تمثّل هذه السمة المعادلات النسبية. على سبيل المثال: ‎5/(x - 3) = 2/(x - 1)
Rational Expression

تمثّل هذه السمة التعبيرات النسبية. على سبيل المثال: ‎1/(x^3 + 4x^2 + 5x + 2)
Rational Inequality

تمثّل هذه السمة المتباينات النسبية. على سبيل المثال: ‎5/(x - 3) > 2/(x - 1)
Slope

تمثّل هذه السمة مسائل الميل. على سبيل المثال: أوجِد الميل في y = 10x + 5.
Statistics

مسائل الإحصاءات على سبيل المثال: أوجِد متوسط مجموعة من الأرقام (3، 8، 2، 10)
System of Equations

مسائل المعادلات المترابطة على سبيل المثال: أوجِد حلّاً للمعادلة التالية2x + 5y = 16;3x - 5y = - 1.
Trigonometry

أوجِد حلّ جيب(t) + جيب تمام(t) = 1.