adstock_decay_spec パラメータを設定する

一般的に、メディアは KPI に遅延効果をもたらし、時間の経過とともに効果は徐々に減少します。この遅延効果をモデル化するために、次の Adstock 関数を使用して特定のチャネルのメディア施策を変換します。

$$ \text{Adstock}(x_t, x_{t-1}, \cdots, x_{t-L};\ \alpha)\ = \dfrac{\sum\limits_{s=0}^L\ w(s; \alpha)x_{t-s}} {\sum\limits _{s=0}^L\ w(s; \alpha)} $$

各記号は以下を表します。

  • \(w(s; \alpha) \) : 負ではない重み付け関数

  • \(x_s \geq 0\) : 時間 \(s\)でのメディア施策

  • \(\alpha\ \in\ [0, 1]\) : 減衰パラメータ

  • \(L\) : 最大遅延時間

メリディアンには 2 通りの減衰曲線が用意されています。幾何級数的減衰曲線と二項減衰曲線です。メディア効果の減衰率は、選択した関数と学習したパラメータ α によって決まります。ModelSpec の adstock_decay_spec パラメータは、使用する関数または関数の組み合わせを定義します。たとえば、すべてのチャネルで二項減衰を使用するには、次のように指定します。

from meridian.model import spec
model_spec = spec.ModelSpec(
  adstock_decay_spec='binomial'
)

"Channel0"、"Channel1"、"Channel2" という 3 つのチャネルでそれぞれ二項減衰、幾何級数的減衰、二項減衰を使用するには、次のように指定します。

from meridian.model import spec
model_spec = spec.ModelSpec(
  adstock_decay_spec=dict(
    Channel0='binomial',
    Channel1='geometric',
    Channel2='binomial',
  )
)

一般的に、メディア チャネルの遅延効果の大部分が効果期間の後半まで持続すると考えられる場合は二項減衰、それ以外の場合は幾何級数的減衰の使用をおすすめします。

これらの関数は、Adstock 関数の重み \(w(s; \alpha)\) を定義します。時間 \(t\)において、時間 \(t-s\) のメディア施策の重みが \(w(s; \alpha) / \sum_{s\in{\{0, ..., L\}}}w(s; \alpha)\)になるように定義されます。Adstock 関数について詳しくは、メディアの飽和と遅延をご覧ください。

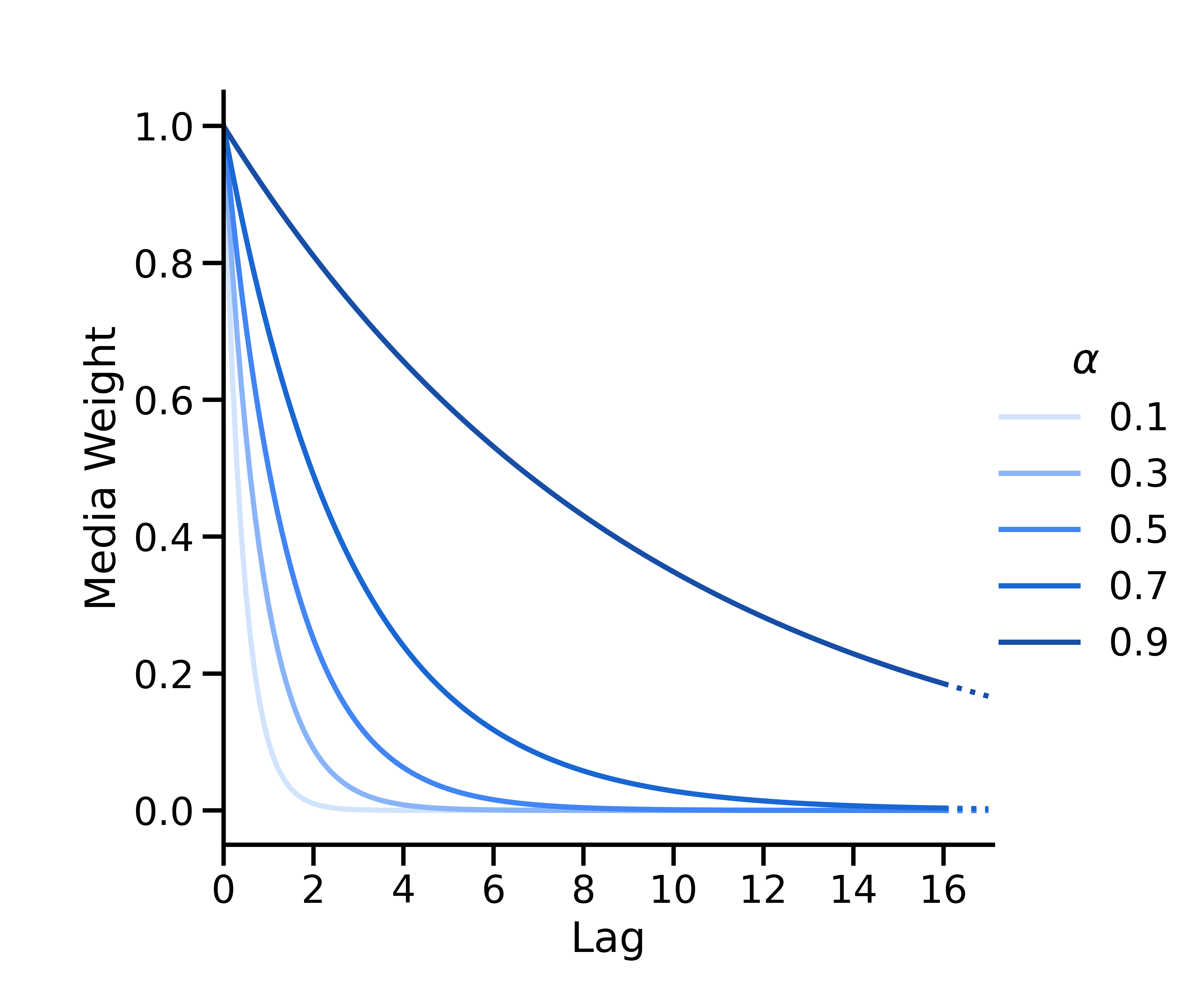
幾何級数的減衰

幾何級数的減衰は \(w(s; \alpha) = \alpha^s\)としてパラメータ化されます。\(\alpha \in [0, 1] \) は減衰率を示す幾何級数的なパラメータ、\(s\) は遅延です。時間 \(t\)では、時間 \(t-s\) のメディア施策の重みは \(w(s; \alpha) = \alpha^s\)になります。この重みは、すべての重みの合計が 1 になるように正規化されます。

幾何級数的減衰の例。

二項減衰

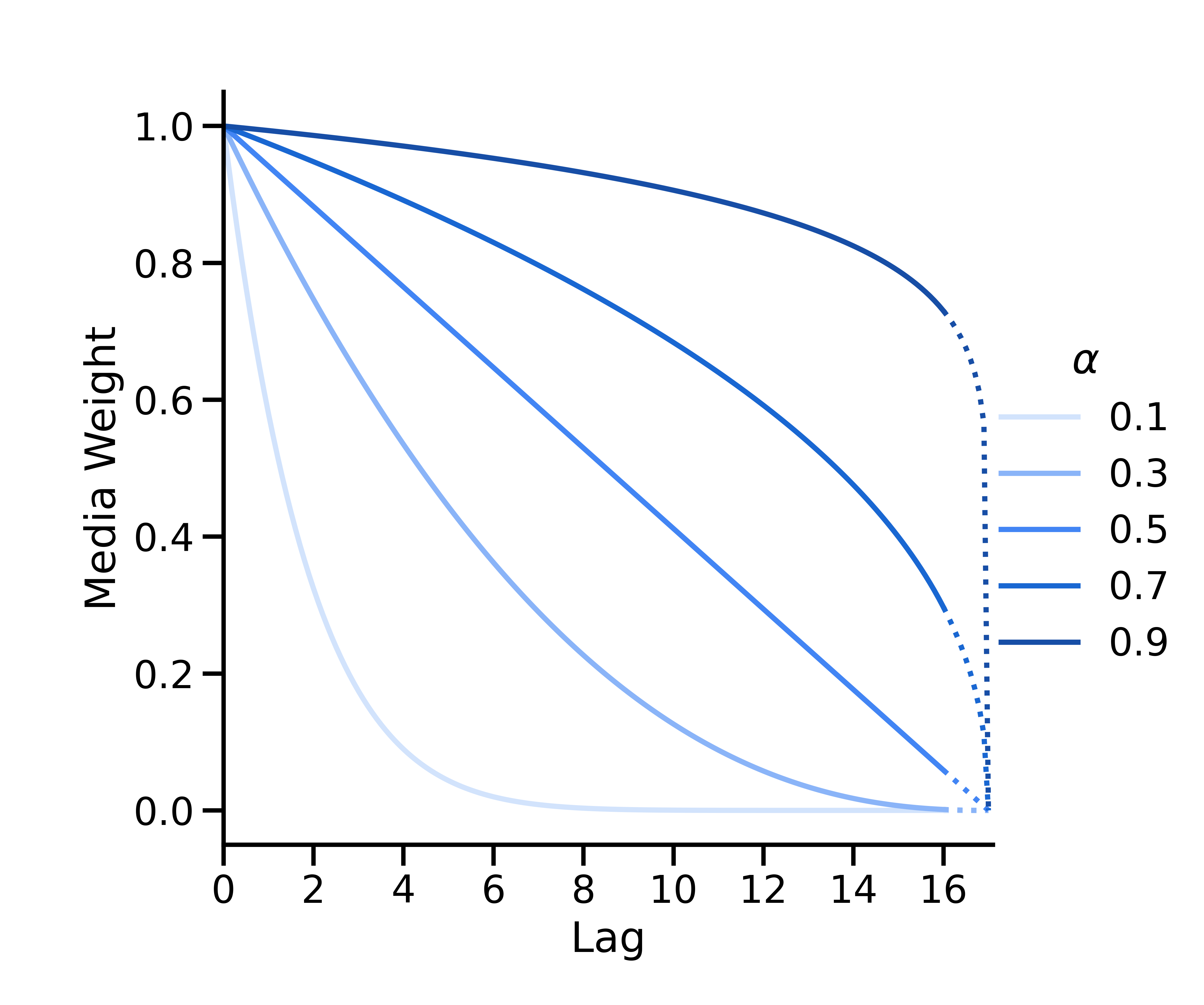
二項減衰は次のようにパラメータ化されます。

$$ w(s; \alpha) = \left(1 - \frac{s}{1 + L}\right)^{\alpha_*}, \\ \alpha_* = \frac{1}{\alpha} - 1 $$

\(L\) は最大遅延（ModelSpec の max_lag パラメータ）です。マッピング \(\alpha_*=\frac{1}{\alpha} - 1\) は、 \([0, 1]\) から \([0, \infty)\)までの\(\alpha\) の値をマッピングするために使用されます。

二項曲線は、 \(\alpha < 0.5\)の場合は凸状、 \(\alpha = 0.5\)の場合は直線、 \(\alpha > 0.5\)の場合は凹状になります。x 切片が常に \(L + 1\)になるように定義されています。

二項減衰の例。

幾何級数的減衰と二項減衰のどちらを使用するかを決定する

チャネルの効果の大部分が効果期間の後半に集中すると考えられる場合は、二項減衰を選択することをおすすめします。それ以外の場合は幾何級数的減衰を選択します。

減衰曲線は、遅延があるメディアの相対的な重みに影響します。後の期間の相対的な重みを増やすと、必然的に前の期間の相対的な重みが減少します。二項減衰曲線は、幾何級数的曲線よりも緩やかにゼロに減衰する重みを定義します。そのため、二項減衰曲線では、チャネルのすべてのメディア効果の大部分が期間の後半に集中する傾向があり、幾何級数的減衰曲線では、期間の前半に集中する傾向があります。二項減衰曲線は、x 切片が常に \(L + 1\)になり、効果期間をカバーするように「引き伸ばされる」ことから、比較的大きい max_lag 値を使用する場合に適しています。詳しくは、max_lag パラメータを設定するをご覧ください。

二項減衰曲線は比較的大きい max_lag 値をサポートできるため、すべてのチャネルで選択したくなるかもしれません。ただし、すべてのチャネルが二項減衰曲線で最適にモデル化されるわけではありません。二項減衰曲線は、効果期間の後半に効果の大部分が集中すると考えられるチャネルに最適です。二項減衰曲線が適していないチャネルで使用すると、短期的な効果が過小評価される可能性があります。

関数 幾何級数的 二項
推奨メディア 効果の持続時間が短いメディア 効果期間の後半まで効果が持続するメディア
曲線の形状 急速な減衰 減衰までに時間がかかる可能性
最大遅延の推奨値 2～10（期間） 4～20（期間）
デメリット 長期的な効果が過小評価される可能性 短期的な効果が過小評価される可能性

長期的な効果に関する考慮事項

モデルで網羅しきれない長期的な効果が考えられる場合は、二項減衰曲線、アルファの事前分布の変更、max_lag の変更を組み合わせると効果的です。media_effects.plot_adstock_decay() の事前分布曲線を使用して、max_lag、アルファ事前分布、減衰関数がどのように相互作用するかを確認します。その後、これらを微調整して、遅延効果に関する最初の仮説にモデルを一致させることができます。事前分布と max_lag の変更は、特定の減衰関数を選択するのと並行して、またはその代わりに実施できます。収束、モデルの適合度、効果期間のバランスが取れるよう、さまざまな組み合わせを試すことをおすすめします。max_lag 値の選択について詳しくは、max_lag パラメータを設定するをご覧ください。

アルファ事前分布

メリディアンのデフォルトのアルファ事前分布は \(U(0, 1)\)です。これは、幾何級数的減衰関数と二項減衰関数の両方に対する無情報事前分布です。特定のチャネルのメディア効果が減衰する速度について、おおよその値がわかっている場合は、そのチャネルにカスタムのアルファ事前分布を設定して、おおよその値をメリディアンに提供できます。

幾何級数的減衰と二項減衰の両方で、\(\alpha\) とメディア効果の減衰率の間には単調な関係があります。 \(\alpha\)が小さいほど減衰が速く、 \(\alpha\) が大きいほど減衰が遅くなります。幾何級数的関数と二項関数はどちらも、 \(\alpha=0\)のときに短期的な効果を最大化します。この場合、遅延効果はありません。また、 \(\alpha=1\)のときに長期的な効果を最大化します。この場合、過去の遅延期間内のすべてのメディアが均等に重み付けされます。

そのため、ゼロに近い質量でアルファ事前分布を設定し、減衰を速めて効果を短期間で得られるようにすることをおすすめします。減衰を遅くして効果を長期間持続させるには、1 に近い質量で事前分布を設定することをおすすめします。

二項 \(\alpha\) のマッピング

二項関数は \(\alpha_* \in [0, \infty)\) で減衰し、幾何級数的関数は \(\alpha \in [0, 1]\)で減衰するため、マッピング \(\alpha_*: [0, 1]\rightarrow[0, \infty) \) が実行されます。このマッピングにより、区間 \([0, 1]\) で定義された事前分布を二項の場合に \([0, \infty)\) に正しく変換し、幾何級数的減衰とモデル仕様との整合性を維持できます。アルファの値が小さいほど減衰が速く、効果が短期的になり、アルファの値が大きいほど減衰が遅く、効果が長期的になることを意味します。

高度なオプション: 二項を使用する場合にカスタムの事前分布を直接 \(\alpha_*\) に設定する

メリディアンは、幾何級数的関数と二項関数の両方で、 \(\alpha\) に \(U(0, 1)\) のデフォルトの事前分布を使用します。二項減衰では、\(\alpha\) の \(U(0, 1)\) 事前分布は、 \(\alpha_*\)の Lomax(1, 1) 事前分布と同等です。

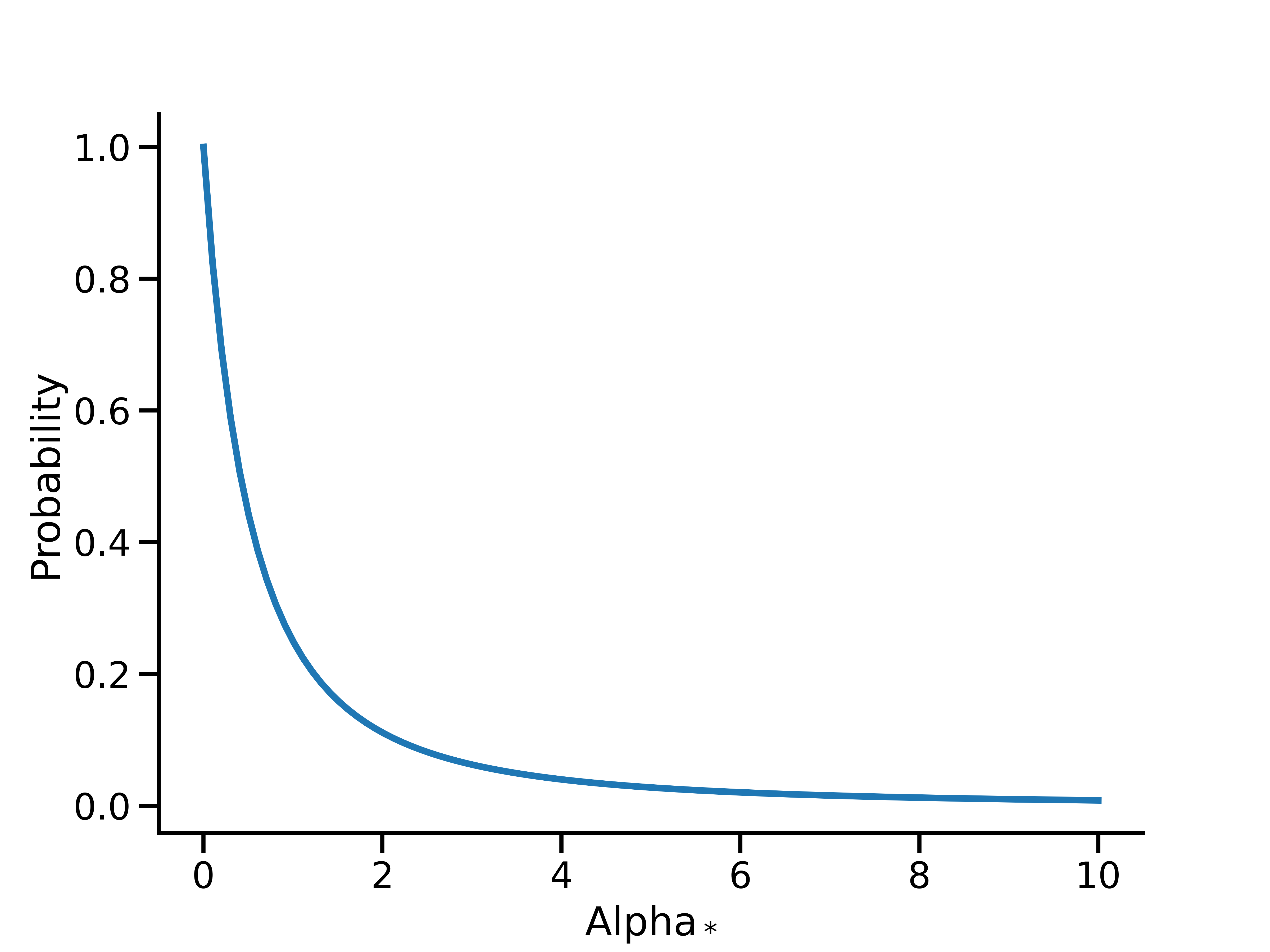
二項を使用する場合のアルファ スター事前分布。

これは、二項減衰率をデータから判断するには、比較的情報量の少ない事前分布のままです。

メリディアンは、カスタムの \(\alpha\) 事前分布に \([0, 1]\) のサポート（ベータ分布など）があることを想定しています。この事前分布は、 \(1/x-1\)を使用して負ではない実数にマッピングされます。ただし、 \([0, \infty)\) のサポートを使用して \(\alpha_*\) の事前分布を定義する場合は、逆マッピング \(\frac{1}{1+x}\)を使用して変換できます。このマッピングは、ヘルパー メソッド adstock_hill.transform_non_negative_reals_distribution を介して利用可能です。たとえば、平均が 0.5 で分散が 0.5 の \(\alpha_*\) の対数正規事前分布を得る場合は次のようになります。

import tensorflow as tf

# Example: pick mu, sigma so that the mean, variance of alpha_* are both 0.5
mu = -tf.math.log(2.0) - 0.5 * tf.math.log(3.0)
sigma = tf.math.sqrt(tf.math.log(3.0))

alpha_star_prior = tfp.distributions.LogNormal(mu, sigma)  # prior on alpha_* for binomial
alpha_prior = adstock_hill.transform_non_negative_reals_distribution(alpha_star_prior)

prior = prior_distribution.PriorDistribution(
  alpha=alpha_prior
)

model_spec = spec.ModelSpec(
  prior=prior,
  adstock_decay_spec='binomial'
)

その後、アルファ事前分布を直接調べることも可能です。たとえば、アルファの確率密度関数を表示する場合は次のようになります。

import numpy as np
from matplotlib import pyplot as plt

x = np.linspace(0, 1, 100)
fig, ax = plt.subplots(figsize=(8, 6))
ax.plot(x, alpha_prior.prob(x), linewidth=3)
ax.set(xlabel='Alpha', ylabel='Probability')
plt.show()

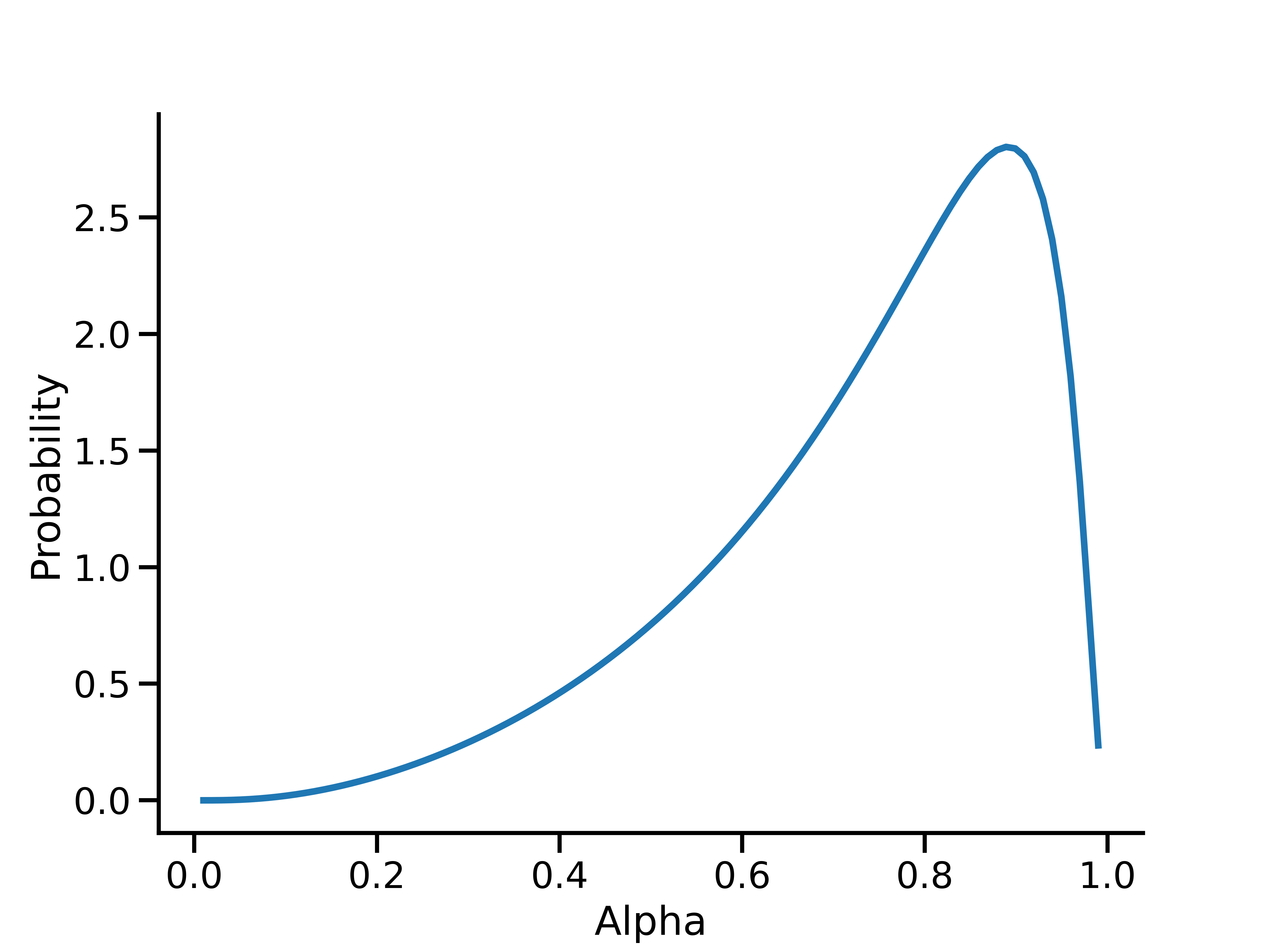
メリディアンでマッピングすると LogNormal(-log 2 - 0.5 log 3, sqrt(log(3))) になるアルファ分布の確率密度。

このプロットは、\(\alpha_*\) の対数正規事前分布（平均と分散がそれぞれ 0.5 と 0.5）につながる \(\alpha\) の事前分布を示しています。