En général, le média a un effet différé sur le KPI, et cet effet s'atténue sur la durée. Pour modéliser cet effet différé, nous transformons l'exécution média d'un canal donné à l'aide de la fonction Adstock ci-dessous :
où :
\(w(s; \alpha) \) est une fonction de pondération non négative ;
\(x_s \geq 0\) correspond à l'exécution média à l'instant \(s\) ;
\(\alpha\ \in\ [0, 1]\) est le paramètre de régression ;
\(L\) est la durée maximale de latence.
Meridian propose deux courbes de régression : géométrique et binomiale. Le taux d'atténuation de l'effet média dépend de la fonction choisie et du paramètre alpha appris. Le paramètre adstock_decay_spec de ModelSpec détermine quelle fonction ou combinaison de fonctions sont utilisées.
Par exemple, afin d'utiliser la régression binomiale pour tous les canaux, vous pouvez spécifier :
from meridian.model import spec
model_spec = spec.ModelSpec(
adstock_decay_spec='binomial'
)
En revanche, afin d'utiliser respectivement la régression binomiale, la régression géométrique et la régression binomiale pour trois canaux nommés "Channel0", "Channel1" et "Channel2", vous pouvez spécifier :
from meridian.model import spec
model_spec = spec.ModelSpec(
adstock_decay_spec=dict(
Channel0='binomial',
Channel1='geometric',
Channel2='binomial',
)
)
En général, nous vous recommandons d'utiliser la régression binomiale lorsque vous pensez qu'une proportion importante des effets différés d'un canal média durent jusqu'à la seconde moitié de la période d'effet. Dans le cas contraire, nous vous recommandons d'utiliser la régression géométrique.
Ces fonctions définissent les pondérations \(w(s; \alpha)\) pour la fonction Adstock. Elles sont définies de sorte qu'à l'instant \(t\), une pondération de \(w(s; \alpha) / \sum_{s\in{\{0, ..., L\}}}w(s; \alpha)\)soit appliquée à l'exécution média à l'instant \(t-s\) . Pour en savoir plus sur la fonction Adstock, consultez Latence et saturation des canaux média.
Régression géométrique
La régression géométrique est paramétrée sous la forme \(w(s; \alpha) = \alpha^s\), où\(\alpha \in [0, 1] \) est le paramètre géométrique indiquant le taux de régression et\(s\) correspond à la latence. À l'instant \(t\), l'exécution média à l'instant \(t-s\) a une pondération de \(w(s; \alpha) = \alpha^s\), qui est ensuite normalisée de sorte que la somme de toutes les pondérations soit égale à 1.
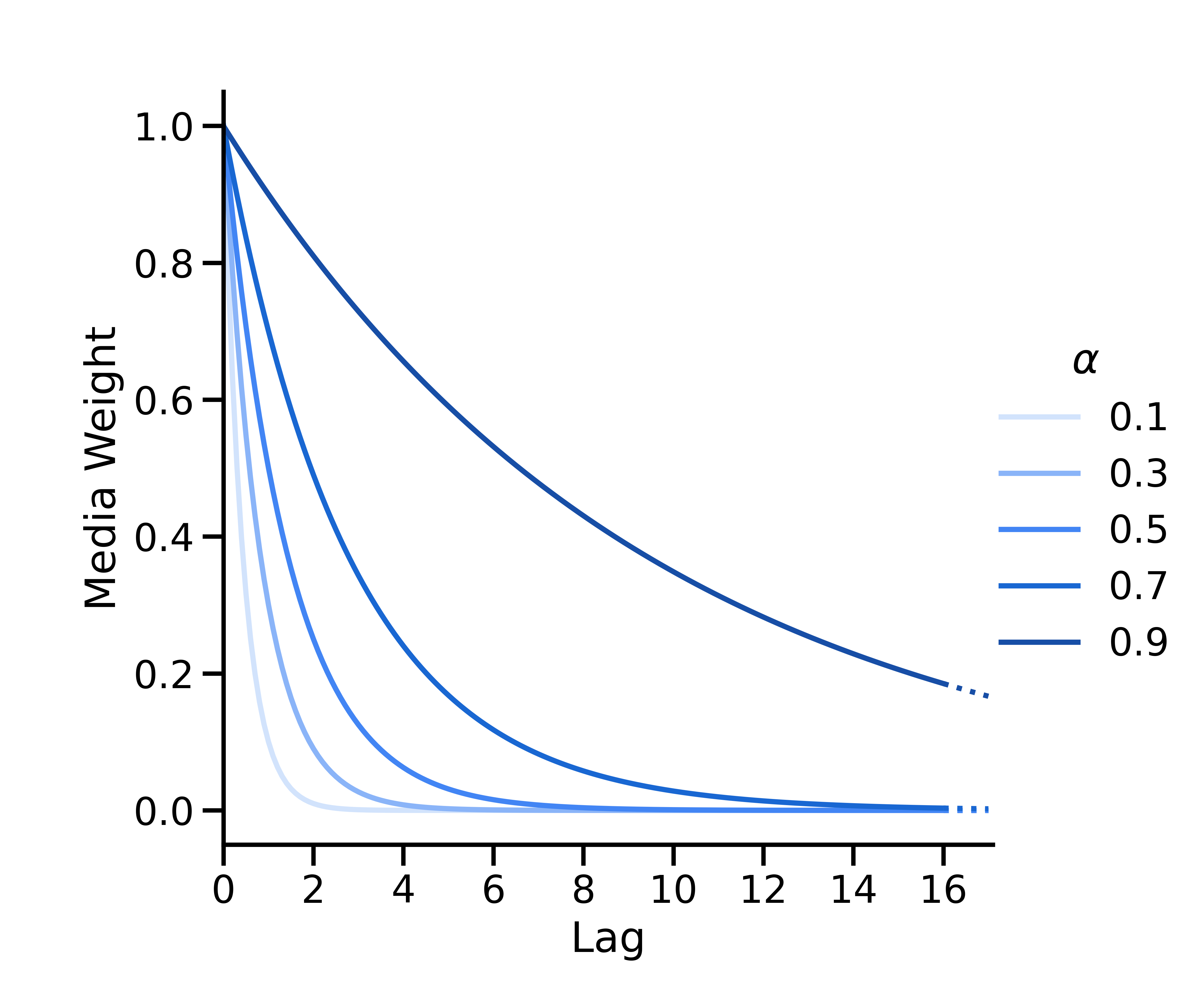
Régression binomiale
La régression binomiale est paramétrée comme suit :
où \(L\) correspond à la latence maximale (paramètre max_lag de ModelSpec). Le mappage \(\alpha_*=\frac{1}{\alpha} - 1\) permet de mapper les valeurs de\(\alpha\) de \([0, 1]\) à \([0, \infty)\).
La courbe binomiale est convexe si \(\alpha < 0.5\), linéaire si \(\alpha = 0.5\)et concave si \(\alpha > 0.5\). Elle est définie de sorte que son abscisse à l'origine corresponde toujours à \(L + 1\).
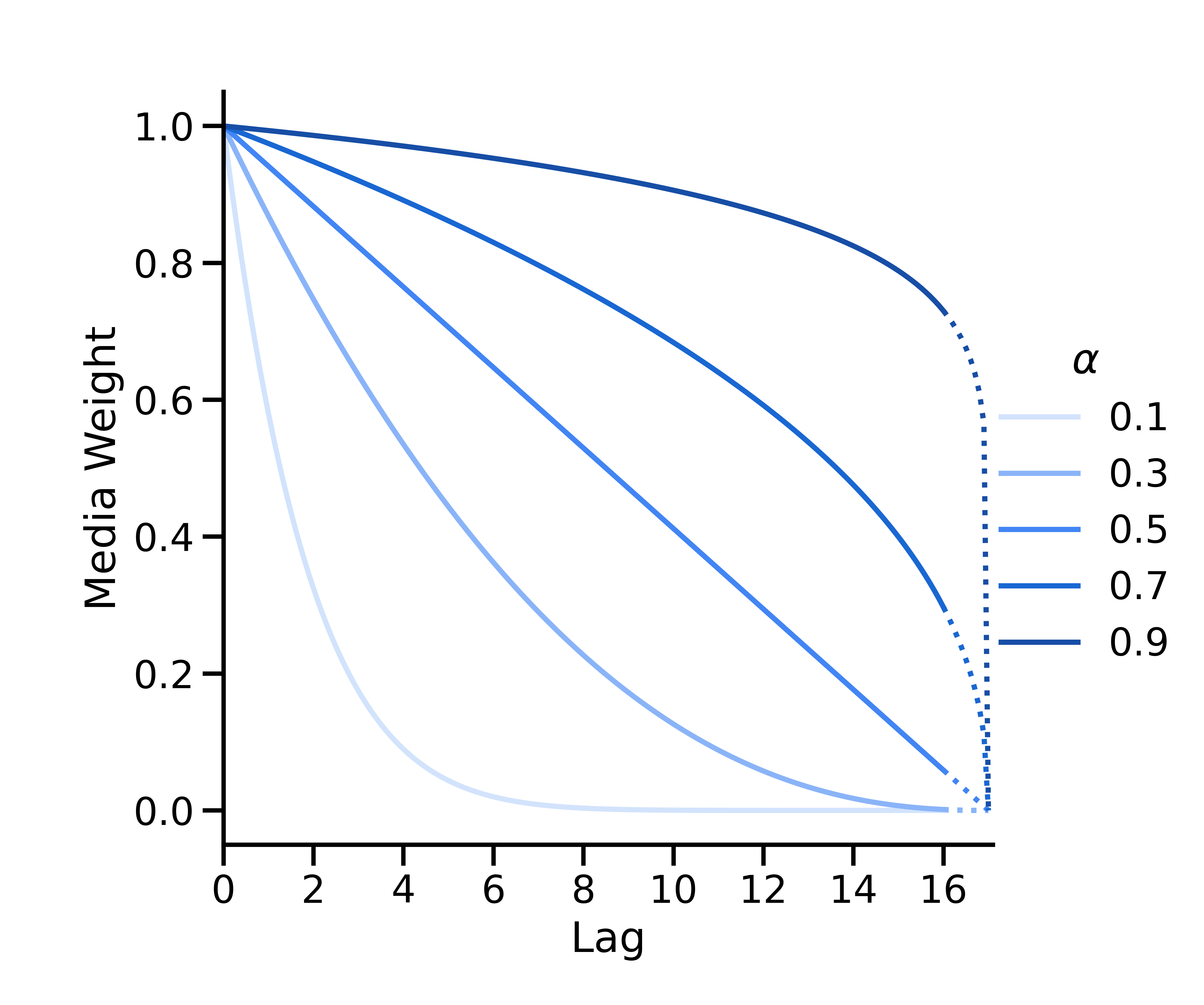
Choisir entre la régression géométrique et la régression binomiale
Nous vous recommandons de sélectionner la régression binomiale si vous pensez qu'une part importante des effets d'un canal ont lieu lors de la seconde moitié de la période d'effet. Dans le cas contraire, choisissez la régression géométrique.
La courbe de régression affecte les pondérations relatives de l'effet média différé. Si vous augmentez la pondération relative des périodes ultérieures, vous diminuez nécessairement celle des périodes antérieures. La courbe de régression binomiale définit des pondérations qui diminuent jusqu'à zéro plus progressivement que la courbe géométrique. Par conséquent, la courbe de régression binomiale encourage une plus grande part de l'effet média total d'un canal à se produire au cours des périodes ultérieures, tandis que la courbe de régression géométrique encourage une plus grande part de l'effet média total d'un canal à se produire au cours des périodes antérieures. Choisissez la courbe de régression binomiale si vous utilisez des valeurs plus élevées de max_lag, car elle est "étirée" pour couvrir la période d'effet, comme son abscisse à l'origine correspond toujours à \(L + 1\). Pour en savoir plus, consultez Définir le paramètre max_lag.
Il peut être tentant de sélectionner la courbe de régression binomiale pour tous les canaux en raison de sa capacité à prendre en charge des valeurs max_lag plus élevées. Toutefois, n'oubliez pas que la courbe de régression binomiale n'est pas toujours la meilleure option pour modéliser les canaux. Elle est plus adaptée lorsque vous pensez qu'une part importante des effets d'un canal ont lieu lors de la seconde moitié de la période d'effet. Une mauvaise application de la courbe de régression binomiale peut entraîner une sous-estimation des effets à court terme.
| Fonction | Géométrique | Binomiale |
|---|---|---|
| Recommandée pour | Les médias avec effets de courte durée | Les médias avec effets qui durent jusqu'à la seconde moitié de la période d'effet |
| Forme de la courbe | Régression rapide | Peut durer plus longtemps avant de régresser |
| Latence maximale recommandée | 2-10 périodes | 4-20 périodes |
| Inconvénients | Risque de sous-estimation des effets à long terme | Risque de sous-estimation des effets à court terme |
Considérations concernant les effets à long terme
Si vous vous attendez à des effets à long terme qui ne se matérialisent pas dans un modèle, il peut être utile de combiner la courbe de régression binomiale en modifiant l'a priori sur alpha et la max_lag. Utilisez les courbes a priori de media_effects.plot_adstock_decay() pour voir comment la max_lag, l'a priori alpha et la fonction de régression interagissent entre eux. Vous pouvez ensuite les affiner pour aligner un modèle sur vos hypothèses initiales concernant les effets différés. Vous pouvez modifier l'a priori et la max_lag en plus ou au lieu de sélectionner une fonction de régression spécifique. Nous vous recommandons de tester différentes combinaisons pour équilibrer la convergence, l'adéquation du modèle et la période d'effet. Pour en savoir plus sur la façon de sélectionner une valeur de max_lag, consultez Définir le paramètre max_lag.
L'a priori alpha
Dans Meridian, l'a priori alpha par défaut est \(U(0, 1)\). Il s'agit d'un a priori non informatif pour les fonctions de régression géométrique et de régression binomiale. Si vous avez une idée du taux d'atténuation de l'effet média pour un canal spécifique, vous pouvez définir un a priori alpha personnalisé sur ce canal pour en informer Meridian.
Pour la régression géométrique et la régression binomiale, il existe une relation monotone entre\(\alpha\) et le taux de régression de l'effet média : plus \(\alpha\)est petit, plus la régression est rapide, et plus \(\alpha\) est grand, plus la régression est courte. Les fonctions géométriques et binomiales maximisent toutes deux les effets à court terme lorsque \(\alpha=0\), auquel cas il n'y a pas d'effets différés. Elles maximisent les effets à long terme lorsque \(\alpha=1\), auquel cas tous les médias de la période historique différée sont pondérés de manière égale.
Par conséquent, nous vous recommandons de définir un a priori sur alpha avec une plus grande part de sa masse proche de 0 pour favoriser une régression plus rapide et des effets à plus court terme. Nous vous recommandons de définir un a priori avec une plus grande part de sa masse proche de 1 pour favoriser une régression plus lente et des effets à plus long terme.
La carte \(\alpha\) binomiale
Le mappage \(\alpha_*: [0, 1]\rightarrow[0, \infty) \) est effectué, car la fonction binomiale régresse pour \(\alpha_* \in [0, \infty)\) , tandis que la fonction géométrique régresse pour \(\alpha \in [0, 1]\). Ce mappage permet de traduire correctement les a priori définis sur l'intervalle \([0, 1]\) en \([0, \infty)\) dans le cas binomial et de conserver la cohérence de la spécification du modèle avec la régression géométrique. Notez que des valeurs alpha faibles impliquent une régression rapide et des effets à plus court terme, tandis que des valeurs alpha élevées impliquent une régression lente et des effets à plus long terme.
Option avancée : définir un a priori personnalisé directement sur \(\alpha_*\) lorsque vous utilisez la fonction binomiale
Meridian utilise un a priori par défaut de \(U(0, 1)\) sur \(\alpha\) pour les fonctions géométriques et pour les fonctions binomiales. Avec la régression binomiale, un a priori \(U(0, 1)\) sur\(\alpha\) équivaut à un a priori Lomax(1, 1) sur \(\alpha_*\):
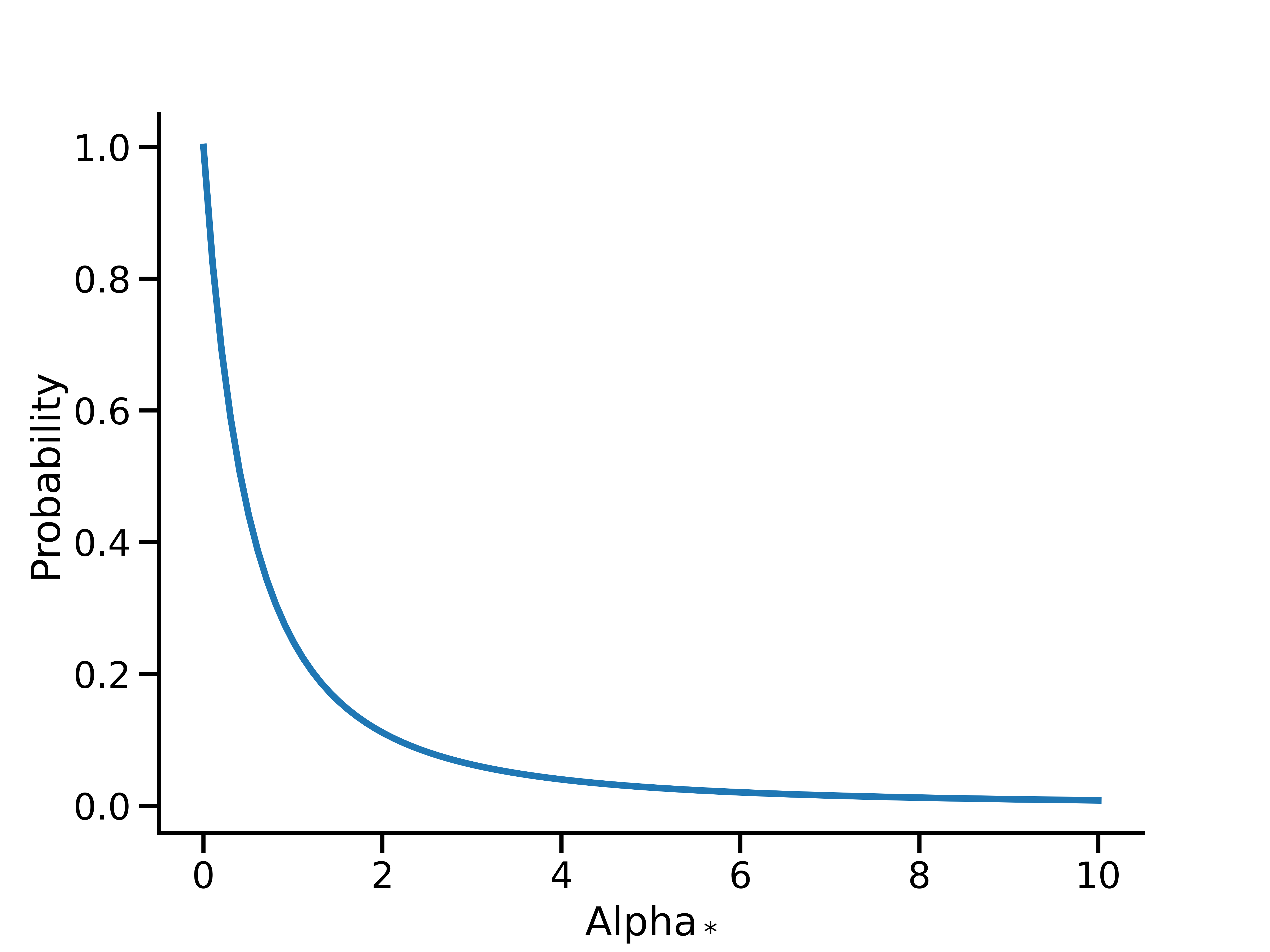
Il s'agit d'un a priori relativement peu informatif pour permettre aux données d'orienter le taux de régression avec la régression binomiale.
Meridian s'attend à ce que les a priori \(\alpha\) personnalisés prennent en charge \([0, 1]\) (par exemple, une distribution bêta) qui sera ensuite mappé sur les nombres réels non négatifs avec \(1/x-1\). Toutefois, si vous souhaitez pouvoir définir un a priori sur \(\alpha_*\) avec la prise en charge de \([0, \infty)\) , vous pouvez le faire, puis le transformer avec le mappage inverse \(\frac{1}{1+x}\). Ce mappage est disponible avec la méthode d'aide adstock_hill.transform_non_negative_reals_distribution.
Par exemple, pour obtenir un a priori lognormal sur \(\alpha_*\) avec une moyenne de 0,5 et une variance de 0,5 :
import tensorflow as tf
# Example: pick mu, sigma so that the mean, variance of alpha_* are both 0.5
mu = -tf.math.log(2.0) - 0.5 * tf.math.log(3.0)
sigma = tf.math.sqrt(tf.math.log(3.0))
alpha_star_prior = tfp.distributions.LogNormal(mu, sigma) # prior on alpha_* for binomial
alpha_prior = adstock_hill.transform_non_negative_reals_distribution(alpha_star_prior)
prior = prior_distribution.PriorDistribution(
alpha=alpha_prior
)
model_spec = spec.ModelSpec(
prior=prior,
adstock_decay_spec='binomial'
)
Vous pouvez ensuite interroger directement l'a priori alpha. Par exemple, pour voir la fonction de densité de probabilité sur alpha :
import numpy as np
from matplotlib import pyplot as plt
x = np.linspace(0, 1, 100)
fig, ax = plt.subplots(figsize=(8, 6))
ax.plot(x, alpha_prior.prob(x), linewidth=3)
ax.set(xlabel='Alpha', ylabel='Probability')
plt.show()
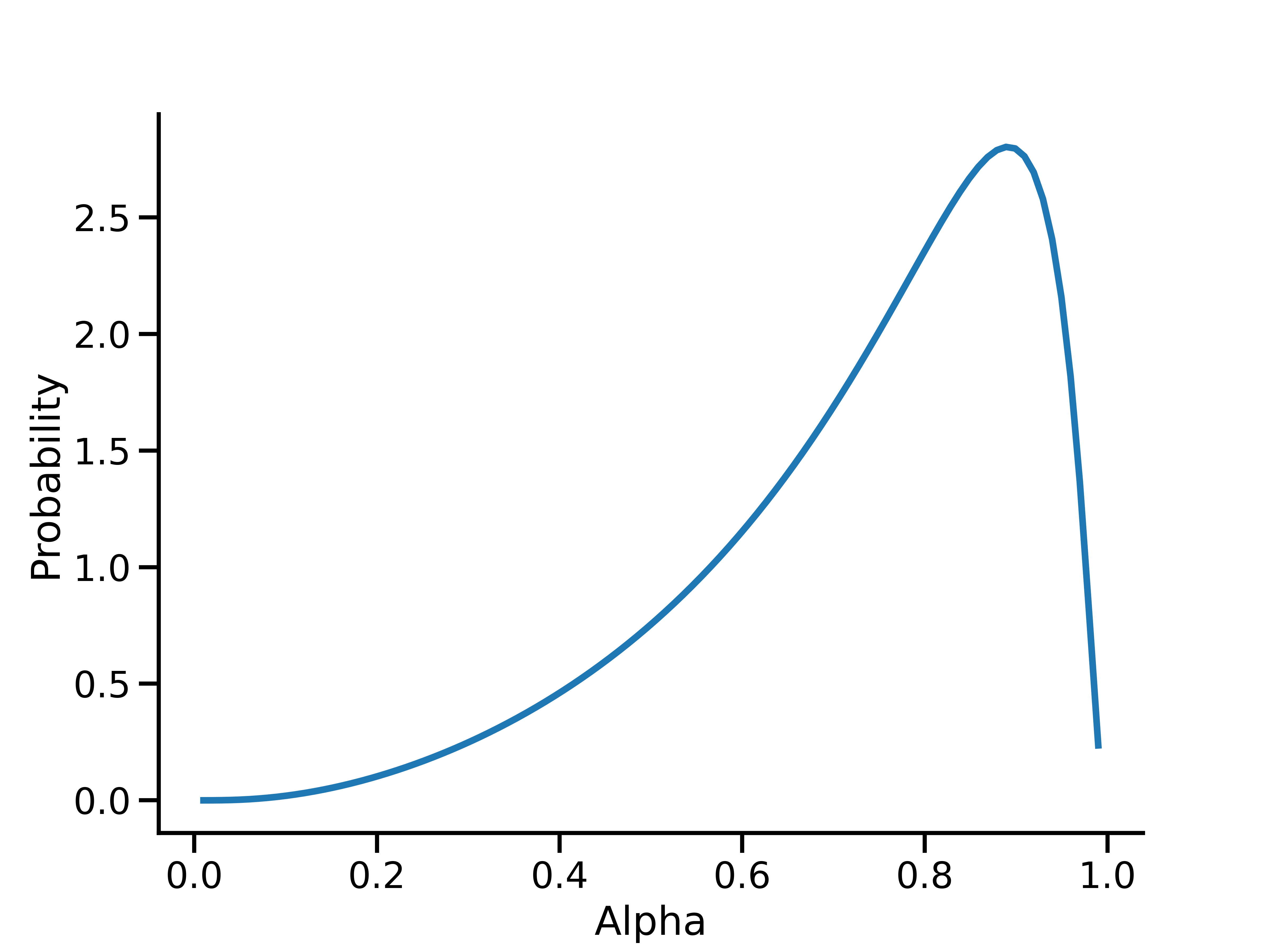
Ce graphique montre l'a priori sur \(\alpha\) qui conduit à un a priori lognormal sur\(\alpha_*\) avec une moyenne et une variance de 0,5 et 0,5 respectivement.