Introduction to Priors

In Marketing Mix Modeling, a common challenge is ensuring the model's results reflect the complex reality of your business powerful Bayesian feature: priors. This page provides a high-level introduction to what priors are, why they are a cornerstone of Meridian's methodology, and key considerations for using them.

What Are Priors?

A "prior" is information you provide to the model before it analyzes your data. Think of it as giving the model a head start or some expert advice based on your business knowledge, industry benchmarks, or results from past experiments. This relationship is at the heart of Bayesian statistics and can be summarized as:

\[ \underset{\text{(the model)}}{\text{Posterior}} \propto \underset{\text{(the data)}}{\text{Likelihood}} \cdot \underset{\text{(your belief)}}{\text{Prior}} \]

The model's posterior distribution, from which estimates are derived, takes into consideration both your initial beliefs (the prior) and what the data itself suggests (the likelihood).The prior stabilizes your model while keeping it grounded in real-world business context.

A key feature of Meridian is its ability to work directly with the business metrics you care about. Instead of requiring prior information about abstract regression coefficients, Meridian is structured to incorporate prior information about tangible and measurable metrics like Return on Investment (ROI), Marginal Return on Investment (mROI), and contribution percentage.

A prior can come from many sources:

• Results from past incrementality experiments (for example, lift tests or geo-experiments).
• Industry benchmarks.
• Previous MMM results.
• Your team's own subject matter expertise.

If you don't have any, don't worry. Meridian has inbuilt defaults which can give you a jumping off point.

Understand Priors in terms of Distributions

To gain an intuitive understanding of priors, we present some visual examples for how you can translate your business intuition into priors for your MMM.

What a Prior Distribution Looks Like

Priors are expressed as probability distributions. A distribution assigns a density (relative likelihood) to every possible value of a parameter, such as ROI. The area under the curve between any two points on the x-axis represents the probability that the true value falls within that range. For example, the following distribution plot shows that values between -1 and 1 are much more likely than values outside that range. For a Normal distribution with mean = 0 and standard deviation = 1 , there is a 68.3% probability that the true value lies between -1 and 1.

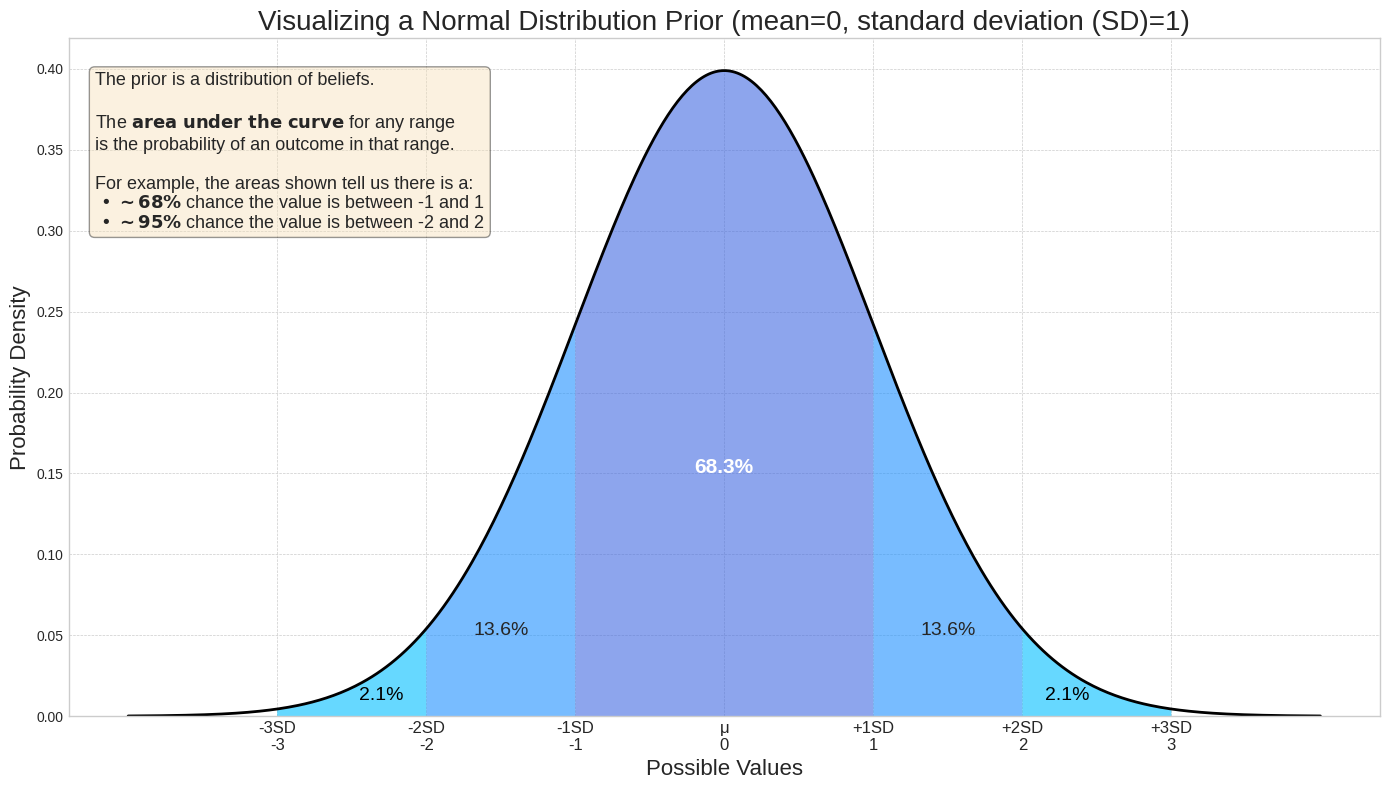
The effect of standard deviation on confidence

The standard deviation controls the width of the distribution and reflects your confidence in the parameter value. A smaller standard deviation concentrates the probability around the parameter value, indicating higher confidence, while a larger standard deviation spreads the probability out, indicating more uncertainty.

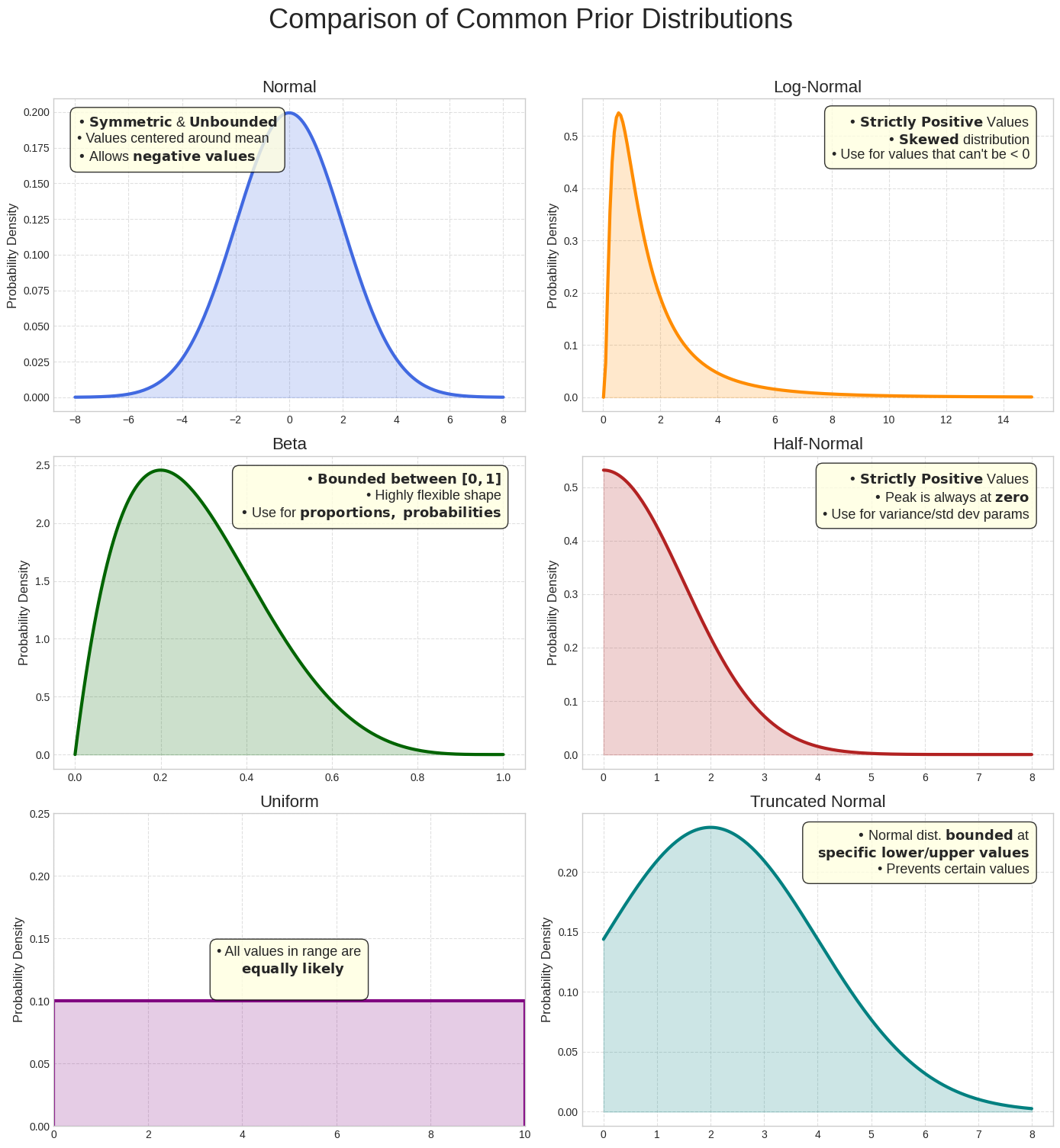
Comparison of Common Prior Distributions

While the Normal distribution is a useful illustration, other distributions are often more suitable depending on the parameter being modeled. For example, since ROI should be positive, a distribution that only assigns probability to positive values—like the Log-Normal or Half-Normal—is often a better choice than a Normal distribution, which allows for negative values. Meridian uses several common distributions, allowing you to select the one that best reflects the nature of the parameter you are modeling.

An Example in Code: Confidence versus Uncertainty

Here's how you might express different levels of belief about the ROI for three different paid media channels in your code.

from meridian.model import prior_distribution

# --- Channel 1: High Confidence ---
# You have strong experiment results showing ROI is consistently around 1.2.
# You use a small standard deviation (0.2) to reflect your high confidence.
strong_prior_channel_1 = prior_distribution.lognormal_dist_from_mean_std(
    mean=1.2,
    std=0.2
)

# --- Channel 2: Low Confidence ---
# You have weaker experiment results showing ROI is around 1.0.
# You use a small sigma (0.9) to reflect your weaker confidence in the
# experiment result than for Channel 1.
weak_prior_channel_2 = prior_distribution.lognormal_dist_from_mean_std(
    mean=1.0,
    std=0.9
)

# --- Channel 3: Confidence in a range ---
# You believe there's a 95% chance the ROI is between 2.0 and 6.0.
range_prior_channel_3 = prior_distribution.lognormal_dist_from_range(
    low=2.0,
    high=6.0
    mass_percent=0.95
)

# You would then assign these distributions to their respective channels
# when you configure your model.
prior_config = prior_distribution.PriorDistribution(
    roi_m=[strong_prior_channel_1, weaker_prior_channel_2, range_prior_channel_3]
)

Visualize Your Priors

Plotting your priors is straightforward and can help ensure that your priors match your intuition.

from matplotlib import pyplot as plt
from meridian.model import prior_distribution
import numpy as np

# Define the LogNormal distribution
lognormal_dist = prior_distribution.lognormal_dist_from_mean_std(2.0, 0.5)
# Plot a histogram of samples from the LogNormal distribution
plt.hist(lognormal_dist.sample(1000))

Why Priors Matter

Using priors is more than just a technical feature; it is fundamental to getting causal estimates that you can trust and act on.

• More Plausible and Stable Results with Less Data: Aggregated marketing data can be sparse or noisy. Priors provide a stabilizing effect, guiding the model toward plausible outcomes and preventing it from reaching incorrect conclusions based on limited data.
• Results Grounded in Business Reality: By incorporating knowledge from trusted sources like lift studies, the prior's stabilizing effect guides the model into alignment with this knowledge, increasing stakeholder confidence.
• Encoding Business Intuition: You almost always have some intuition about your business. For example, it may be rare to get an ROI greater than 6.0 in your industry. You can encode this intuition in your prior to guide the model toward more realistic results, even if you don't have hard data from an experiment.
• Intuitive Model Controls: Setting a prior is like having an intuitive conversation with your model. Instead of tweaking abstract parameters, you are providing guidance in a language you understand, such as, "I have strong evidence that the ROI for my channel is around 1.5."