Stay organized with collections
Save and categorize content based on your preferences.
Many problems in computer science can be represented by a graph consisting of
nodes and links between them. Examples are network flow problems, which
involve transporting goods or material across a network, such as a railway system.
You can represent a network flow by a graph whose nodes are cities and whose
arcs are rail lines between them. (They're called flows because their
properties are similar to those of water flowing through a network of pipes.)
A key constraint in network flows is that each arc has a capacity —
the maximum amount that can be transported across the arc in a fixed period of
time.
The maximum flow problem is to determine the maximum total amount that can
be transported across all arcs in the network, subject to the capacity
constraints.
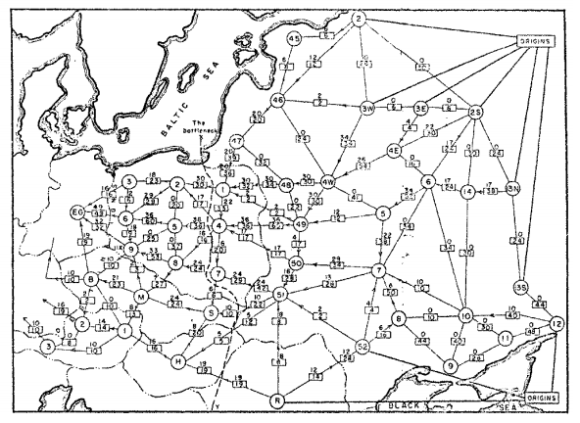
The first person to study this problem was the Russian mathematician A.N.
Tolstoi, in the 1930s. The map below shows the actual railway network for which
he wanted to find a maximum flow.
OR-Tools provides several solvers for network flow problems in its
graph libraries.
The following sections present examples of network flow problems and show how to
solve them:
[[["Easy to understand","easyToUnderstand","thumb-up"],["Solved my problem","solvedMyProblem","thumb-up"],["Other","otherUp","thumb-up"]],[["Missing the information I need","missingTheInformationINeed","thumb-down"],["Too complicated / too many steps","tooComplicatedTooManySteps","thumb-down"],["Out of date","outOfDate","thumb-down"],["Samples / code issue","samplesCodeIssue","thumb-down"],["Other","otherDown","thumb-down"]],["Last updated 2024-08-28 UTC."],[[["Network flow problems, like transporting goods across a railway system, can be represented by graphs with nodes and links, where links have capacity limits."],["The maximum flow problem aims to find the maximum transportable amount across a network, respecting capacity constraints."],["OR-Tools offers various solvers in its graph libraries to address network flow problems like maximum flows and minimum cost flows."],["Example applications of network flows include assignments with individual workers or teams, solvable using OR-Tools."]]],["Computer science utilizes graphs to model problems like network flow, where goods are transported across a network (e.g., railway). Each link (arc) in the network has a capacity, limiting transport volume. The maximum flow problem determines the highest total transport volume across all arcs, respecting these capacity constraints. This problem, first studied by A.N. Tolstoi, can be solved using solvers from the OR-Tools graph libraries, which are useful for problems such as maximum flows, minimum cost flows, and assignment problems.\n"]]
