В следующих разделах мы проиллюстрируем программирование в ограничениях (CP) комбинаторной задачей, основанной на игре в шахматы. В шахматах ферзь может атаковать по горизонтали, вертикали и диагонали. Проблема N-ферзей спрашивает:
Как можно разместить N ферзей на шахматной доске NxN так, чтобы никакие два из них не атаковали друг друга?
Ниже вы можете увидеть одно из возможных решений проблемы N-ферзей для N = 4.
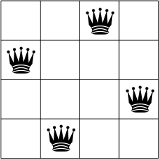
Никакие два ферзя не находятся в одной строке, столбце или диагонали.
Обратите внимание, что это не проблема оптимизации: мы хотим найти все возможные решения, а не одно оптимальное решение, что делает его естественным кандидатом для программирования в ограничениях. В следующих разделах описан подход CP к проблеме N-ферзей и представлены программы, которые решают ее с использованием как решателя CP-SAT, так и исходного решателя CP.
CP-подход к проблеме N-ферзей
Решатель CP работает, систематически перебирая все возможные присвоения значений переменным в задаче, чтобы найти возможные решения. В задаче с четырьмя ферзями решатель начинает с крайнего левого столбца и последовательно размещает по одному ферзя в каждом столбце в месте, которое не подвергается атаке ранее размещенных ферзей.
Распространение и возврат
В поиске программирования с ограничениями есть два ключевых элемента:
- Распространение . Каждый раз, когда решатель присваивает значение переменной, ограничения добавляют ограничения на возможные значения неназначенных переменных. Эти ограничения распространяются на будущие назначения переменных. Например, в задаче с четырьмя ферзями каждый раз, когда решатель ставит ферзя, он не может размещать других ферзей на ряду и диагоналях, на которых находится текущий ферзь. Распространение может значительно ускорить поиск за счет сокращения набора значений переменных, которые должен исследовать решатель.
- Возврат происходит, когда либо решатель не может присвоить значение следующей переменной из-за ограничений, либо находит решение. В любом случае решатель возвращается к предыдущему этапу и меняет значение переменной на этом этапе на значение, которое еще не использовалось. В примере с четырьмя ферзями это означает перемещение ферзя на новое поле текущего столбца.
Далее вы увидите, как программирование с ограничениями использует распространение и возврат для решения проблемы четырех ферзей.
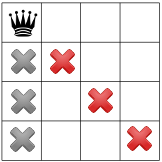
Предположим, что решатель начинает с произвольного размещения ферзя в верхнем левом углу. Это своего рода гипотеза; возможно, окажется, что с ферзем в левом верхнем углу решения не существует.
Учитывая эту гипотезу, какие ограничения мы можем распространить? Одно ограничение состоит в том, что в столбце может быть только один ферзь (серые крестики внизу), а другое ограничение запрещает наличие двух ферзей на одной диагонали (красные крестики внизу).
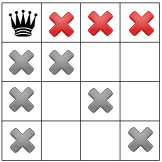
Наше третье ограничение запрещает ферзям находиться в одном ряду:
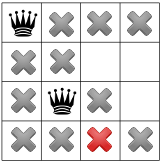
Наши ограничения распространились, и мы можем проверить другую гипотезу и разместить второго ферзя на одном из доступных оставшихся полей. Наш решатель может решить поместить в него первый доступный квадрат во втором столбце:
После распространения диагонального ограничения мы видим, что оно не оставляет свободных квадратов ни в третьем столбце, ни в последней строке:
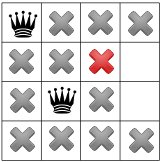
Поскольку на данном этапе решения невозможны, нам необходимо отступить. Один из вариантов заключается в том, чтобы решатель выбрал другой доступный квадрат во втором столбце. Однако распространение ограничения затем заставляет ферзя оказаться во второй строке третьего столбца, не оставляя подходящих мест для четвертого ферзя:

Итак, решатель должен снова вернуться, на этот раз обратно к месту расположения первого ферзя. Мы только что показали, что никакое решение проблемы ферзей не будет занимать угловое поле.
Поскольку в углу не может быть ферзя, решатель перемещает первого ферзя на одного вниз и распространяется, оставляя только одно место для второго ферзя:
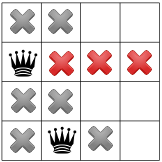
Повторное размножение показывает, что для третьей королевы осталось только одно место:
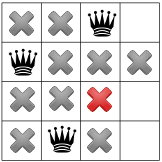
И для четвертой и последней королевы:

У нас есть первое решение! Если бы мы приказали нашему решателю остановиться после нахождения первого решения, он бы закончился здесь. В противном случае он снова отступит и поместит первого ферзя в третью строку первого столбца.
Решение с использованием CP-SAT
Задача N-ферзей идеально подходит для программирования в ограничениях. В этом разделе мы рассмотрим короткую программу Python, которая использует решатель CP-SAT для поиска всех решений проблемы.
Импортируйте библиотеки
Следующий код импортирует необходимую библиотеку.
Питон
import sys import time from ortools.sat.python import cp_model
С++
#include <stdlib.h> #include <sstream> #include <string> #include <vector> #include "absl/strings/numbers.h" #include "ortools/base/logging.h" #include "ortools/sat/cp_model.h" #include "ortools/sat/cp_model.pb.h" #include "ortools/sat/cp_model_solver.h" #include "ortools/sat/model.h" #include "ortools/sat/sat_parameters.pb.h" #include "ortools/util/sorted_interval_list.h"
Ява
import com.google.ortools.Loader; import com.google.ortools.sat.CpModel; import com.google.ortools.sat.CpSolver; import com.google.ortools.sat.CpSolverSolutionCallback; import com.google.ortools.sat.IntVar; import com.google.ortools.sat.LinearExpr;
С#
using System; using Google.OrTools.Sat;
Объявить модель
Следующий код объявляет модель CP-SAT.
Питон
model = cp_model.CpModel()
С++
CpModelBuilder cp_model;
Ява
CpModel model = new CpModel();
С#
CpModel model = new CpModel();
int BoardSize = 8;
// There are `BoardSize` number of variables, one for a queen in each
// column of the board. The value of each variable is the row that the
// queen is in.
IntVar[] queens = new IntVar[BoardSize];
for (int i = 0; i < BoardSize; ++i)
{
queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}");
}
// Define constraints.
// All rows must be different.
model.AddAllDifferent(queens);
// No two queens can be on the same diagonal.
LinearExpr[] diag1 = new LinearExpr[BoardSize];
LinearExpr[] diag2 = new LinearExpr[BoardSize];
for (int i = 0; i < BoardSize; ++i)
{
diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i);
diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i);
}
model.AddAllDifferent(diag1);
model.AddAllDifferent(diag2);
// Creates a solver and solves the model.
CpSolver solver = new CpSolver();
SolutionPrinter cb = new SolutionPrinter(queens);
// Search for all solutions.
solver.StringParameters = "enumerate_all_solutions:true";
// And solve.
solver.Solve(model, cb);
Console.WriteLine("Statistics");
Console.WriteLine($" conflicts : {solver.NumConflicts()}");
Console.WriteLine($" branches : {solver.NumBranches()}");
Console.WriteLine($" wall time : {solver.WallTime()} s");
Console.WriteLine($" number of solutions found: {cb.SolutionCount()}");
}
}
Создайте переменные
Решатель создает переменные для задачи в виде массива с именем queens .
Питон
# There are `board_size` number of variables, one for a queen in each column
# of the board. The value of each variable is the row that the queen is in.
queens = [model.new_int_var(0, board_size - 1, f"x_{i}") for i in range(board_size)]С++
// There are `board_size` number of variables, one for a queen in each column
// of the board. The value of each variable is the row that the queen is in.
std::vector<IntVar> queens;
queens.reserve(board_size);
Domain range(0, board_size - 1);
for (int i = 0; i < board_size; ++i) {
queens.push_back(
cp_model.NewIntVar(range).WithName("x" + std::to_string(i)));
}Ява
int boardSize = 8;
// There are `BoardSize` number of variables, one for a queen in each column of the board. The
// value of each variable is the row that the queen is in.
IntVar[] queens = new IntVar[boardSize];
for (int i = 0; i < boardSize; ++i) {
queens[i] = model.newIntVar(0, boardSize - 1, "x" + i);
}С#
int BoardSize = 8;
// There are `BoardSize` number of variables, one for a queen in each
// column of the board. The value of each variable is the row that the
// queen is in.
IntVar[] queens = new IntVar[BoardSize];
for (int i = 0; i < BoardSize; ++i)
{
queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}");
} Здесь мы предполагаем, что queens[j] — это номер строки для ферзя в столбце j . Другими словами, queens[j] = i означает, что в строке i и столбце j есть ферзь.
Создайте ограничения
Вот код, который создает ограничения для проблемы.
Питон
# All rows must be different. model.add_all_different(queens) # No two queens can be on the same diagonal. model.add_all_different(queens[i] + i for i in range(board_size)) model.add_all_different(queens[i] - i for i in range(board_size))
С++
// The following sets the constraint that all queens are in different rows.
cp_model.AddAllDifferent(queens);
// No two queens can be on the same diagonal.
std::vector<LinearExpr> diag_1;
diag_1.reserve(board_size);
std::vector<LinearExpr> diag_2;
diag_2.reserve(board_size);
for (int i = 0; i < board_size; ++i) {
diag_1.push_back(queens[i] + i);
diag_2.push_back(queens[i] - i);
}
cp_model.AddAllDifferent(diag_1);
cp_model.AddAllDifferent(diag_2);Ява
// All rows must be different.
model.addAllDifferent(queens);
// No two queens can be on the same diagonal.
LinearExpr[] diag1 = new LinearExpr[boardSize];
LinearExpr[] diag2 = new LinearExpr[boardSize];
for (int i = 0; i < boardSize; ++i) {
diag1[i] = LinearExpr.newBuilder().add(queens[i]).add(i).build();
diag2[i] = LinearExpr.newBuilder().add(queens[i]).add(-i).build();
}
model.addAllDifferent(diag1);
model.addAllDifferent(diag2);С#
// All rows must be different.
model.AddAllDifferent(queens);
// No two queens can be on the same diagonal.
LinearExpr[] diag1 = new LinearExpr[BoardSize];
LinearExpr[] diag2 = new LinearExpr[BoardSize];
for (int i = 0; i < BoardSize; ++i)
{
diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i);
diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i);
}
model.AddAllDifferent(diag1);
model.AddAllDifferent(diag2); В коде используется метод AddAllDifferent , который требует, чтобы все элементы массива переменных были разными.
Давайте посмотрим, как эти ограничения гарантируют выполнение трех условий задачи N-ферзей (ферзи в разных строках, столбцах и диагоналях).
Никаких двух ферзей в одном ряду
Применение метода AllDifferent решателя к queens приводит к тому, что значения queens[j] будут разными для каждого j , а это означает, что все ферзи должны находиться в разных строках.
Никаких двух ферзей в одной колонне
Это ограничение неявно присутствует в определении queens . Поскольку никакие два элемента queens не могут иметь одинаковый индекс, никакие два ферзя не могут находиться в одном столбце.
Нет двух ферзей на одной диагонали
Диагональное ограничение немного сложнее, чем ограничение строки и столбца. Во-первых, если два ферзя лежат на одной диагонали, должно выполняться одно из следующих условий:
- Номер строки плюс номер столбца для каждого из двух ферзей равны. Другими словами,
queens(j) + jимеет одно и то же значение для двух разных индексовj. - Номер строки минус номер столбца для каждого из двух ферзей равны. В этом случае
queens(j) - jимеет одно и то же значение для двух разных индексовj.
Одно из этих условий означает, что ферзи лежат на одной восходящей диагонали (слева направо), а другое означает, что они лежат на одной нисходящей диагонали. Какое условие соответствует возрастанию, а какое убыванию, зависит от того, как вы упорядочите строки и столбцы. Как упоминалось в предыдущем разделе , порядок не влияет на набор решений, а влияет только на то, как вы их визуализируете.
Таким образом, диагональное ограничение заключается в том, что все значения queens(j) + j должны быть разными, а значения queens(j) - j должны быть разными для разных j .
Чтобы применить метод AddAllDifferent к queens(j) + j , мы помещаем N экземпляров переменной для j от 0 до N-1 в массив diag1 следующим образом:
q1 = model.NewIntVar(0, 2 * board_size, 'diag1_%i' % i) diag1.append(q1) model.Add(q1 == queens[j] + j)
Затем мы применяем AddAllDifferent к diag1 .
model.AddAllDifferent(diag1)
Ограничение для queens(j) - j создается аналогично.
Создать принтер решения
Чтобы распечатать все решения задачи N-ферзей, вам необходимо передать обратный вызов, называемый принтером решения , решателю CP-SAT. Обратный вызов печатает каждое новое решение по мере того, как его находит решатель. Следующий код создает принтер решения.
Питон
class NQueenSolutionPrinter(cp_model.CpSolverSolutionCallback):
"""Print intermediate solutions."""
def __init__(self, queens: list[cp_model.IntVar]):
cp_model.CpSolverSolutionCallback.__init__(self)
self.__queens = queens
self.__solution_count = 0
self.__start_time = time.time()
@property
def solution_count(self) -> int:
return self.__solution_count
def on_solution_callback(self):
current_time = time.time()
print(
f"Solution {self.__solution_count}, "
f"time = {current_time - self.__start_time} s"
)
self.__solution_count += 1
all_queens = range(len(self.__queens))
for i in all_queens:
for j in all_queens:
if self.value(self.__queens[j]) == i:
# There is a queen in column j, row i.
print("Q", end=" ")
else:
print("_", end=" ")
print()
print()
С++
int num_solutions = 0;
Model model;
model.Add(NewFeasibleSolutionObserver([&](const CpSolverResponse& response) {
LOG(INFO) << "Solution " << num_solutions;
for (int i = 0; i < board_size; ++i) {
std::stringstream ss;
for (int j = 0; j < board_size; ++j) {
if (SolutionIntegerValue(response, queens[j]) == i) {
// There is a queen in column j, row i.
ss << "Q";
} else {
ss << "_";
}
if (j != board_size - 1) ss << " ";
}
LOG(INFO) << ss.str();
}
num_solutions++;
}));Ява
static class SolutionPrinter extends CpSolverSolutionCallback {
public SolutionPrinter(IntVar[] queensIn) {
solutionCount = 0;
queens = queensIn;
}
@Override
public void onSolutionCallback() {
System.out.println("Solution " + solutionCount);
for (int i = 0; i < queens.length; ++i) {
for (int j = 0; j < queens.length; ++j) {
if (value(queens[j]) == i) {
System.out.print("Q");
} else {
System.out.print("_");
}
if (j != queens.length - 1) {
System.out.print(" ");
}
}
System.out.println();
}
solutionCount++;
}
public int getSolutionCount() {
return solutionCount;
}
private int solutionCount;
private final IntVar[] queens;
}С#
public class SolutionPrinter : CpSolverSolutionCallback
{
public SolutionPrinter(IntVar[] queens)
{
queens_ = queens;
}
public override void OnSolutionCallback()
{
Console.WriteLine($"Solution {SolutionCount_}");
for (int i = 0; i < queens_.Length; ++i)
{
for (int j = 0; j < queens_.Length; ++j)
{
if (Value(queens_[j]) == i)
{
Console.Write("Q");
}
else
{
Console.Write("_");
}
if (j != queens_.Length - 1)
Console.Write(" ");
}
Console.WriteLine("");
}
SolutionCount_++;
}
public int SolutionCount()
{
return SolutionCount_;
}
private int SolutionCount_;
private IntVar[] queens_;
}Обратите внимание, что принтер решения должен быть написан как класс Python из-за интерфейса Python с базовым решателем C++.
Решения печатаются на принтере растворов следующими строками.
for v in self.__variables:
print('%s = %i' % (v, self.Value(v)), end = ' ') В этом примере self.__variables — это переменная queens , и каждый v соответствует одной из восьми записей queens . Это выведет решение в следующем виде: x0 = queens(0) x1 = queens(1) ... x7 = queens(7) где xi — номер столбца ферзя в строке i .
В следующем разделе показан пример решения.
Вызов решателя и отображение результатов
Следующий код запускает решатель и отображает решения.
Питон
solver = cp_model.CpSolver() solution_printer = NQueenSolutionPrinter(queens) solver.parameters.enumerate_all_solutions = True solver.solve(model, solution_printer)
С++
// Tell the solver to enumerate all solutions. SatParameters parameters; parameters.set_enumerate_all_solutions(true); model.Add(NewSatParameters(parameters)); const CpSolverResponse response = SolveCpModel(cp_model.Build(), &model); LOG(INFO) << "Number of solutions found: " << num_solutions;
Ява
CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Tell the solver to enumerate all solutions. solver.getParameters().setEnumerateAllSolutions(true); // And solve. solver.solve(model, cb);
С#
// Creates a solver and solves the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Search for all solutions. solver.StringParameters = "enumerate_all_solutions:true"; // And solve. solver.Solve(model, cb);
Программа находит 92 различных решения для доски 8х8. Вот первый.
Q _ _ _ _ _ _ _
_ _ _ _ _ _ Q _
_ _ _ _ Q _ _ _
_ _ _ _ _ _ _ Q
_ Q _ _ _ _ _ _
_ _ _ Q _ _ _ _
_ _ _ _ _ Q _ _
_ _ Q _ _ _ _ _
...91 other solutions displayed...
Solutions found: 92 Вы можете решить проблему для доски другого размера, передав N в качестве аргумента командной строки. Например, если программа называется queens , python nqueens_sat.py 6 решает проблему для доски 6x6.
Вся программа
Вот вся программа для программы N-queens.
Питон
"""OR-Tools solution to the N-queens problem."""
import sys
import time
from ortools.sat.python import cp_model
class NQueenSolutionPrinter(cp_model.CpSolverSolutionCallback):
"""Print intermediate solutions."""
def __init__(self, queens: list[cp_model.IntVar]):
cp_model.CpSolverSolutionCallback.__init__(self)
self.__queens = queens
self.__solution_count = 0
self.__start_time = time.time()
@property
def solution_count(self) -> int:
return self.__solution_count
def on_solution_callback(self):
current_time = time.time()
print(
f"Solution {self.__solution_count}, "
f"time = {current_time - self.__start_time} s"
)
self.__solution_count += 1
all_queens = range(len(self.__queens))
for i in all_queens:
for j in all_queens:
if self.value(self.__queens[j]) == i:
# There is a queen in column j, row i.
print("Q", end=" ")
else:
print("_", end=" ")
print()
print()
def main(board_size: int) -> None:
# Creates the solver.
model = cp_model.CpModel()
# Creates the variables.
# There are `board_size` number of variables, one for a queen in each column
# of the board. The value of each variable is the row that the queen is in.
queens = [model.new_int_var(0, board_size - 1, f"x_{i}") for i in range(board_size)]
# Creates the constraints.
# All rows must be different.
model.add_all_different(queens)
# No two queens can be on the same diagonal.
model.add_all_different(queens[i] + i for i in range(board_size))
model.add_all_different(queens[i] - i for i in range(board_size))
# Solve the model.
solver = cp_model.CpSolver()
solution_printer = NQueenSolutionPrinter(queens)
solver.parameters.enumerate_all_solutions = True
solver.solve(model, solution_printer)
# Statistics.
print("\nStatistics")
print(f" conflicts : {solver.num_conflicts}")
print(f" branches : {solver.num_branches}")
print(f" wall time : {solver.wall_time} s")
print(f" solutions found: {solution_printer.solution_count}")
if __name__ == "__main__":
# By default, solve the 8x8 problem.
size = 8
if len(sys.argv) > 1:
size = int(sys.argv[1])
main(size)С++
// OR-Tools solution to the N-queens problem.
#include <stdlib.h>
#include <sstream>
#include <string>
#include <vector>
#include "absl/strings/numbers.h"
#include "ortools/base/logging.h"
#include "ortools/sat/cp_model.h"
#include "ortools/sat/cp_model.pb.h"
#include "ortools/sat/cp_model_solver.h"
#include "ortools/sat/model.h"
#include "ortools/sat/sat_parameters.pb.h"
#include "ortools/util/sorted_interval_list.h"
namespace operations_research {
namespace sat {
void NQueensSat(const int board_size) {
// Instantiate the solver.
CpModelBuilder cp_model;
// There are `board_size` number of variables, one for a queen in each column
// of the board. The value of each variable is the row that the queen is in.
std::vector<IntVar> queens;
queens.reserve(board_size);
Domain range(0, board_size - 1);
for (int i = 0; i < board_size; ++i) {
queens.push_back(
cp_model.NewIntVar(range).WithName("x" + std::to_string(i)));
}
// Define constraints.
// The following sets the constraint that all queens are in different rows.
cp_model.AddAllDifferent(queens);
// No two queens can be on the same diagonal.
std::vector<LinearExpr> diag_1;
diag_1.reserve(board_size);
std::vector<LinearExpr> diag_2;
diag_2.reserve(board_size);
for (int i = 0; i < board_size; ++i) {
diag_1.push_back(queens[i] + i);
diag_2.push_back(queens[i] - i);
}
cp_model.AddAllDifferent(diag_1);
cp_model.AddAllDifferent(diag_2);
int num_solutions = 0;
Model model;
model.Add(NewFeasibleSolutionObserver([&](const CpSolverResponse& response) {
LOG(INFO) << "Solution " << num_solutions;
for (int i = 0; i < board_size; ++i) {
std::stringstream ss;
for (int j = 0; j < board_size; ++j) {
if (SolutionIntegerValue(response, queens[j]) == i) {
// There is a queen in column j, row i.
ss << "Q";
} else {
ss << "_";
}
if (j != board_size - 1) ss << " ";
}
LOG(INFO) << ss.str();
}
num_solutions++;
}));
// Tell the solver to enumerate all solutions.
SatParameters parameters;
parameters.set_enumerate_all_solutions(true);
model.Add(NewSatParameters(parameters));
const CpSolverResponse response = SolveCpModel(cp_model.Build(), &model);
LOG(INFO) << "Number of solutions found: " << num_solutions;
// Statistics.
LOG(INFO) << "Statistics";
LOG(INFO) << CpSolverResponseStats(response);
}
} // namespace sat
} // namespace operations_research
int main(int argc, char** argv) {
int board_size = 8;
if (argc > 1) {
if (!absl::SimpleAtoi(argv[1], &board_size)) {
LOG(INFO) << "Cannot parse '" << argv[1]
<< "', using the default value of 8.";
board_size = 8;
}
}
operations_research::sat::NQueensSat(board_size);
return EXIT_SUCCESS;
}Ява
package com.google.ortools.sat.samples;
import com.google.ortools.Loader;
import com.google.ortools.sat.CpModel;
import com.google.ortools.sat.CpSolver;
import com.google.ortools.sat.CpSolverSolutionCallback;
import com.google.ortools.sat.IntVar;
import com.google.ortools.sat.LinearExpr;
/** OR-Tools solution to the N-queens problem. */
public final class NQueensSat {
static class SolutionPrinter extends CpSolverSolutionCallback {
public SolutionPrinter(IntVar[] queensIn) {
solutionCount = 0;
queens = queensIn;
}
@Override
public void onSolutionCallback() {
System.out.println("Solution " + solutionCount);
for (int i = 0; i < queens.length; ++i) {
for (int j = 0; j < queens.length; ++j) {
if (value(queens[j]) == i) {
System.out.print("Q");
} else {
System.out.print("_");
}
if (j != queens.length - 1) {
System.out.print(" ");
}
}
System.out.println();
}
solutionCount++;
}
public int getSolutionCount() {
return solutionCount;
}
private int solutionCount;
private final IntVar[] queens;
}
public static void main(String[] args) {
Loader.loadNativeLibraries();
// Create the model.
CpModel model = new CpModel();
int boardSize = 8;
// There are `BoardSize` number of variables, one for a queen in each column of the board. The
// value of each variable is the row that the queen is in.
IntVar[] queens = new IntVar[boardSize];
for (int i = 0; i < boardSize; ++i) {
queens[i] = model.newIntVar(0, boardSize - 1, "x" + i);
}
// Define constraints.
// All rows must be different.
model.addAllDifferent(queens);
// No two queens can be on the same diagonal.
LinearExpr[] diag1 = new LinearExpr[boardSize];
LinearExpr[] diag2 = new LinearExpr[boardSize];
for (int i = 0; i < boardSize; ++i) {
diag1[i] = LinearExpr.newBuilder().add(queens[i]).add(i).build();
diag2[i] = LinearExpr.newBuilder().add(queens[i]).add(-i).build();
}
model.addAllDifferent(diag1);
model.addAllDifferent(diag2);
// Create a solver and solve the model.
CpSolver solver = new CpSolver();
SolutionPrinter cb = new SolutionPrinter(queens);
// Tell the solver to enumerate all solutions.
solver.getParameters().setEnumerateAllSolutions(true);
// And solve.
solver.solve(model, cb);
// Statistics.
System.out.println("Statistics");
System.out.println(" conflicts : " + solver.numConflicts());
System.out.println(" branches : " + solver.numBranches());
System.out.println(" wall time : " + solver.wallTime() + " s");
System.out.println(" solutions : " + cb.getSolutionCount());
}
private NQueensSat() {}
}С#
// OR-Tools solution to the N-queens problem.
using System;
using Google.OrTools.Sat;
public class NQueensSat
{
public class SolutionPrinter : CpSolverSolutionCallback
{
public SolutionPrinter(IntVar[] queens)
{
queens_ = queens;
}
public override void OnSolutionCallback()
{
Console.WriteLine($"Solution {SolutionCount_}");
for (int i = 0; i < queens_.Length; ++i)
{
for (int j = 0; j < queens_.Length; ++j)
{
if (Value(queens_[j]) == i)
{
Console.Write("Q");
}
else
{
Console.Write("_");
}
if (j != queens_.Length - 1)
Console.Write(" ");
}
Console.WriteLine("");
}
SolutionCount_++;
}
public int SolutionCount()
{
return SolutionCount_;
}
private int SolutionCount_;
private IntVar[] queens_;
}
static void Main()
{
// Constraint programming engine
CpModel model = new CpModel();
int BoardSize = 8;
// There are `BoardSize` number of variables, one for a queen in each
// column of the board. The value of each variable is the row that the
// queen is in.
IntVar[] queens = new IntVar[BoardSize];
for (int i = 0; i < BoardSize; ++i)
{
queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}");
}
// Define constraints.
// All rows must be different.
model.AddAllDifferent(queens);
// No two queens can be on the same diagonal.
LinearExpr[] diag1 = new LinearExpr[BoardSize];
LinearExpr[] diag2 = new LinearExpr[BoardSize];
for (int i = 0; i < BoardSize; ++i)
{
diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i);
diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i);
}
model.AddAllDifferent(diag1);
model.AddAllDifferent(diag2);
// Creates a solver and solves the model.
CpSolver solver = new CpSolver();
SolutionPrinter cb = new SolutionPrinter(queens);
// Search for all solutions.
solver.StringParameters = "enumerate_all_solutions:true";
// And solve.
solver.Solve(model, cb);
Console.WriteLine("Statistics");
Console.WriteLine($" conflicts : {solver.NumConflicts()}");
Console.WriteLine($" branches : {solver.NumBranches()}");
Console.WriteLine($" wall time : {solver.WallTime()} s");
Console.WriteLine($" number of solutions found: {cb.SolutionCount()}");
}
}Решение с использованием оригинального решателя CP
В следующих разделах представлена программа Python, которая решает N-ферзей с использованием оригинального решателя CP. (Однако мы рекомендуем использовать более новый решатель CP-SAT )
Импортируйте библиотеки
Следующий код импортирует необходимую библиотеку.
Питон
import sys from ortools.constraint_solver import pywrapcp
С++
#include <cstdint> #include <cstdlib> #include <sstream> #include <vector> #include "ortools/base/logging.h" #include "ortools/constraint_solver/constraint_solver.h"
Ява
import com.google.ortools.Loader; import com.google.ortools.constraintsolver.DecisionBuilder; import com.google.ortools.constraintsolver.IntVar; import com.google.ortools.constraintsolver.Solver;
С#
using System; using Google.OrTools.ConstraintSolver;
Объявить решатель
Следующий код объявляет исходный решатель CP.
Питон
solver = pywrapcp.Solver("n-queens")С++
Solver solver("N-Queens");Ява
Solver solver = new Solver("N-Queens");С#
Solver solver = new Solver("N-Queens");Создайте переменные
Метод IntVar решателя создает переменные для задачи в виде массива с именем queens .
Питон
# The array index is the column, and the value is the row.
queens = [solver.IntVar(0, board_size - 1, f"x{i}") for i in range(board_size)]С++
std::vector<IntVar*> queens;
queens.reserve(board_size);
for (int i = 0; i < board_size; ++i) {
queens.push_back(
solver.MakeIntVar(0, board_size - 1, absl::StrCat("x", i)));
}Ява
int boardSize = 8;
IntVar[] queens = new IntVar[boardSize];
for (int i = 0; i < boardSize; ++i) {
queens[i] = solver.makeIntVar(0, boardSize - 1, "x" + i);
}С#
const int BoardSize = 8;
IntVar[] queens = new IntVar[BoardSize];
for (int i = 0; i < BoardSize; ++i)
{
queens[i] = solver.MakeIntVar(0, BoardSize - 1, $"x{i}");
} Для любого решения queens[j] = i означает, что в столбце j и строке i есть ферзь.
Создайте ограничения
Вот код, который создает ограничения для проблемы.
Питон
# All rows must be different. solver.Add(solver.AllDifferent(queens)) # No two queens can be on the same diagonal. solver.Add(solver.AllDifferent([queens[i] + i for i in range(board_size)])) solver.Add(solver.AllDifferent([queens[i] - i for i in range(board_size)]))
С++
// The following sets the constraint that all queens are in different rows.
solver.AddConstraint(solver.MakeAllDifferent(queens));
// All columns must be different because the indices of queens are all
// different. No two queens can be on the same diagonal.
std::vector<IntVar*> diag_1;
diag_1.reserve(board_size);
std::vector<IntVar*> diag_2;
diag_2.reserve(board_size);
for (int i = 0; i < board_size; ++i) {
diag_1.push_back(solver.MakeSum(queens[i], i)->Var());
diag_2.push_back(solver.MakeSum(queens[i], -i)->Var());
}
solver.AddConstraint(solver.MakeAllDifferent(diag_1));
solver.AddConstraint(solver.MakeAllDifferent(diag_2));Ява
// All rows must be different.
solver.addConstraint(solver.makeAllDifferent(queens));
// All columns must be different because the indices of queens are all different.
// No two queens can be on the same diagonal.
IntVar[] diag1 = new IntVar[boardSize];
IntVar[] diag2 = new IntVar[boardSize];
for (int i = 0; i < boardSize; ++i) {
diag1[i] = solver.makeSum(queens[i], i).var();
diag2[i] = solver.makeSum(queens[i], -i).var();
}
solver.addConstraint(solver.makeAllDifferent(diag1));
solver.addConstraint(solver.makeAllDifferent(diag2));С#
// All rows must be different.
solver.Add(queens.AllDifferent());
// All columns must be different because the indices of queens are all different.
// No two queens can be on the same diagonal.
IntVar[] diag1 = new IntVar[BoardSize];
IntVar[] diag2 = new IntVar[BoardSize];
for (int i = 0; i < BoardSize; ++i)
{
diag1[i] = solver.MakeSum(queens[i], i).Var();
diag2[i] = solver.MakeSum(queens[i], -i).Var();
}
solver.Add(diag1.AllDifferent());
solver.Add(diag2.AllDifferent());Эти ограничения гарантируют выполнение трех условий задачи N-ферзей (ферзи в разных строках, столбцах и диагоналях).
Никаких двух ферзей в одном ряду
Применение метода AllDifferent решателя к queens приводит к тому, что значения queens[j] будут разными для каждого j , а это означает, что все ферзи должны находиться в разных строках.
Никаких двух ферзей в одной колонне
Это ограничение неявно присутствует в определении queens . Поскольку никакие два элемента queens не могут иметь одинаковый индекс, никакие два ферзя не могут находиться в одном столбце.
Нет двух ферзей на одной диагонали
Диагональное ограничение немного сложнее, чем ограничение строки и столбца. Во-первых, если два ферзя лежат на одной диагонали, должно выполняться одно из следующих условий:
- Если диагональ нисходящая (идет слева направо), номер строки плюс номер столбца для каждого из двух ферзей равны. Таким образом
queens(i) + iимеет одно и то же значение для двух разных индексовi. - Если диагональ возрастает, то номер строки минус номер столбца для каждого из двух ферзей равны. В этом случае
queens(i) - iимеет одно и то же значение для двух разных индексовi.
Таким образом, диагональное ограничение состоит в том, что все значения queens(i) + i должны быть разными, и точно так же значения queens(i) - i должны быть разными для разных i .
Приведенный выше код добавляет это ограничение, применяя метод AllDifferent к queens[j] + j и queens[j] - j для каждого i .
Добавьте конструктор решений
Следующим шагом является создание конструктора решений, который задает стратегию поиска проблемы. Стратегия поиска может существенно повлиять на время поиска из-за распространения ограничений, что уменьшает количество значений переменных, которые должен исследовать решатель. Вы уже видели пример этого в примере с 4 ферзями .
Следующий код создает построитель решений с использованием метода Phase решателя.
Питон
db = solver.Phase(queens, solver.CHOOSE_FIRST_UNBOUND, solver.ASSIGN_MIN_VALUE)
С++
DecisionBuilder* const db = solver.MakePhase(
queens, Solver::CHOOSE_FIRST_UNBOUND, Solver::ASSIGN_MIN_VALUE);Ява
// Create the decision builder to search for solutions.
final DecisionBuilder db =
solver.makePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);С#
// Create the decision builder to search for solutions. DecisionBuilder db = solver.MakePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);
Подробную информацию о входных аргументах метода Phase см. в разделе «Построитель решений» .
Как работает построитель решений в примере с 4 ферзями
Давайте посмотрим, как конструктор решений направляет поиск на примере с 4 ферзями . Решатель начинается с queens[0] , первой переменной в массиве, как указано CHOOSE_FIRST_UNBOUND . Затем решатель присваивает queens[0] наименьшее значение, которое еще не было опробовано, которое на данном этапе равно 0, в соответствии с указаниями ASSIGN_MIN_VALUE . В результате первый ферзь окажется в левом верхнем углу доски.
Затем решатель выбирает queens[1] , которая теперь является первой несвязанной переменной в queens . После распространения ограничений в столбце 1 есть две возможные строки для ферзя: строка 2 или строка 3. Опция ASSIGN_MIN_VALUE предписывает решателю назначить queens[1] = 2 . (Если вместо этого вы установите IntValueStrategy на ASSIGN_MAX_VALUE , решатель присвоит queens[1] = 3 .)
Вы можете проверить, что остальная часть поиска следует тем же правилам.
Вызов решателя и отображение результатов
Следующий код запускает решатель и отображает решение.
Питон
# Iterates through the solutions, displaying each.
num_solutions = 0
solver.NewSearch(db)
while solver.NextSolution():
# Displays the solution just computed.
for i in range(board_size):
for j in range(board_size):
if queens[j].Value() == i:
# There is a queen in column j, row i.
print("Q", end=" ")
else:
print("_", end=" ")
print()
print()
num_solutions += 1
solver.EndSearch()С++
// Iterates through the solutions, displaying each.
int num_solutions = 0;
solver.NewSearch(db);
while (solver.NextSolution()) {
// Displays the solution just computed.
LOG(INFO) << "Solution " << num_solutions;
for (int i = 0; i < board_size; ++i) {
std::stringstream ss;
for (int j = 0; j < board_size; ++j) {
if (queens[j]->Value() == i) {
// There is a queen in column j, row i.
ss << "Q";
} else {
ss << "_";
}
if (j != board_size - 1) ss << " ";
}
LOG(INFO) << ss.str();
}
num_solutions++;
}
solver.EndSearch();Ява
int solutionCount = 0;
solver.newSearch(db);
while (solver.nextSolution()) {
System.out.println("Solution " + solutionCount);
for (int i = 0; i < boardSize; ++i) {
for (int j = 0; j < boardSize; ++j) {
if (queens[j].value() == i) {
System.out.print("Q");
} else {
System.out.print("_");
}
if (j != boardSize - 1) {
System.out.print(" ");
}
}
System.out.println();
}
solutionCount++;
}
solver.endSearch();С#
// Iterates through the solutions, displaying each.
int SolutionCount = 0;
solver.NewSearch(db);
while (solver.NextSolution())
{
Console.WriteLine("Solution " + SolutionCount);
for (int i = 0; i < BoardSize; ++i)
{
for (int j = 0; j < BoardSize; ++j)
{
if (queens[j].Value() == i)
{
Console.Write("Q");
}
else
{
Console.Write("_");
}
if (j != BoardSize - 1)
Console.Write(" ");
}
Console.WriteLine("");
}
SolutionCount++;
}
solver.EndSearch();Вот первое решение, найденное программой для платы 8х8.
Q _ _ _ _ _ _ _
_ _ _ _ _ _ Q _
_ _ _ _ Q _ _ _
_ _ _ _ _ _ _ Q
_ Q _ _ _ _ _ _
_ _ _ Q _ _ _ _
_ _ _ _ _ Q _ _
_ _ Q _ _ _ _ _
...91 other solutions displayed...
Statistics
failures: 304
branches: 790
wall time: 5 ms
Solutions found: 92 Вы можете решить проблему для доски другого размера, передав N в качестве аргумента командной строки. Например, python nqueens_cp.py 6 решает проблему для платы 6x6.
Вся программа
Полная программа представлена ниже.
Питон
"""OR-Tools solution to the N-queens problem."""
import sys
from ortools.constraint_solver import pywrapcp
def main(board_size):
# Creates the solver.
solver = pywrapcp.Solver("n-queens")
# Creates the variables.
# The array index is the column, and the value is the row.
queens = [solver.IntVar(0, board_size - 1, f"x{i}") for i in range(board_size)]
# Creates the constraints.
# All rows must be different.
solver.Add(solver.AllDifferent(queens))
# No two queens can be on the same diagonal.
solver.Add(solver.AllDifferent([queens[i] + i for i in range(board_size)]))
solver.Add(solver.AllDifferent([queens[i] - i for i in range(board_size)]))
db = solver.Phase(queens, solver.CHOOSE_FIRST_UNBOUND, solver.ASSIGN_MIN_VALUE)
# Iterates through the solutions, displaying each.
num_solutions = 0
solver.NewSearch(db)
while solver.NextSolution():
# Displays the solution just computed.
for i in range(board_size):
for j in range(board_size):
if queens[j].Value() == i:
# There is a queen in column j, row i.
print("Q", end=" ")
else:
print("_", end=" ")
print()
print()
num_solutions += 1
solver.EndSearch()
# Statistics.
print("\nStatistics")
print(f" failures: {solver.Failures()}")
print(f" branches: {solver.Branches()}")
print(f" wall time: {solver.WallTime()} ms")
print(f" Solutions found: {num_solutions}")
if __name__ == "__main__":
# By default, solve the 8x8 problem.
size = 8
if len(sys.argv) > 1:
size = int(sys.argv[1])
main(size)С++
// OR-Tools solution to the N-queens problem.
#include <cstdint>
#include <cstdlib>
#include <sstream>
#include <vector>
#include "ortools/base/logging.h"
#include "ortools/constraint_solver/constraint_solver.h"
namespace operations_research {
void NQueensCp(const int board_size) {
// Instantiate the solver.
Solver solver("N-Queens");
std::vector<IntVar*> queens;
queens.reserve(board_size);
for (int i = 0; i < board_size; ++i) {
queens.push_back(
solver.MakeIntVar(0, board_size - 1, absl::StrCat("x", i)));
}
// Define constraints.
// The following sets the constraint that all queens are in different rows.
solver.AddConstraint(solver.MakeAllDifferent(queens));
// All columns must be different because the indices of queens are all
// different. No two queens can be on the same diagonal.
std::vector<IntVar*> diag_1;
diag_1.reserve(board_size);
std::vector<IntVar*> diag_2;
diag_2.reserve(board_size);
for (int i = 0; i < board_size; ++i) {
diag_1.push_back(solver.MakeSum(queens[i], i)->Var());
diag_2.push_back(solver.MakeSum(queens[i], -i)->Var());
}
solver.AddConstraint(solver.MakeAllDifferent(diag_1));
solver.AddConstraint(solver.MakeAllDifferent(diag_2));
DecisionBuilder* const db = solver.MakePhase(
queens, Solver::CHOOSE_FIRST_UNBOUND, Solver::ASSIGN_MIN_VALUE);
// Iterates through the solutions, displaying each.
int num_solutions = 0;
solver.NewSearch(db);
while (solver.NextSolution()) {
// Displays the solution just computed.
LOG(INFO) << "Solution " << num_solutions;
for (int i = 0; i < board_size; ++i) {
std::stringstream ss;
for (int j = 0; j < board_size; ++j) {
if (queens[j]->Value() == i) {
// There is a queen in column j, row i.
ss << "Q";
} else {
ss << "_";
}
if (j != board_size - 1) ss << " ";
}
LOG(INFO) << ss.str();
}
num_solutions++;
}
solver.EndSearch();
// Statistics.
LOG(INFO) << "Statistics";
LOG(INFO) << " failures: " << solver.failures();
LOG(INFO) << " branches: " << solver.branches();
LOG(INFO) << " wall time: " << solver.wall_time() << " ms";
LOG(INFO) << " Solutions found: " << num_solutions;
}
} // namespace operations_research
int main(int argc, char** argv) {
int board_size = 8;
if (argc > 1) {
board_size = std::atoi(argv[1]);
}
operations_research::NQueensCp(board_size);
return EXIT_SUCCESS;
}Ява
// OR-Tools solution to the N-queens problem.
package com.google.ortools.constraintsolver.samples;
import com.google.ortools.Loader;
import com.google.ortools.constraintsolver.DecisionBuilder;
import com.google.ortools.constraintsolver.IntVar;
import com.google.ortools.constraintsolver.Solver;
/** N-Queens Problem. */
public final class NQueensCp {
public static void main(String[] args) {
Loader.loadNativeLibraries();
// Instantiate the solver.
Solver solver = new Solver("N-Queens");
int boardSize = 8;
IntVar[] queens = new IntVar[boardSize];
for (int i = 0; i < boardSize; ++i) {
queens[i] = solver.makeIntVar(0, boardSize - 1, "x" + i);
}
// Define constraints.
// All rows must be different.
solver.addConstraint(solver.makeAllDifferent(queens));
// All columns must be different because the indices of queens are all different.
// No two queens can be on the same diagonal.
IntVar[] diag1 = new IntVar[boardSize];
IntVar[] diag2 = new IntVar[boardSize];
for (int i = 0; i < boardSize; ++i) {
diag1[i] = solver.makeSum(queens[i], i).var();
diag2[i] = solver.makeSum(queens[i], -i).var();
}
solver.addConstraint(solver.makeAllDifferent(diag1));
solver.addConstraint(solver.makeAllDifferent(diag2));
// Create the decision builder to search for solutions.
final DecisionBuilder db =
solver.makePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);
int solutionCount = 0;
solver.newSearch(db);
while (solver.nextSolution()) {
System.out.println("Solution " + solutionCount);
for (int i = 0; i < boardSize; ++i) {
for (int j = 0; j < boardSize; ++j) {
if (queens[j].value() == i) {
System.out.print("Q");
} else {
System.out.print("_");
}
if (j != boardSize - 1) {
System.out.print(" ");
}
}
System.out.println();
}
solutionCount++;
}
solver.endSearch();
// Statistics.
System.out.println("Statistics");
System.out.println(" failures: " + solver.failures());
System.out.println(" branches: " + solver.branches());
System.out.println(" wall time: " + solver.wallTime() + "ms");
System.out.println(" Solutions found: " + solutionCount);
}
private NQueensCp() {}
}С#
// OR-Tools solution to the N-queens problem.
using System;
using Google.OrTools.ConstraintSolver;
public class NQueensCp
{
public static void Main(String[] args)
{
// Instantiate the solver.
Solver solver = new Solver("N-Queens");
const int BoardSize = 8;
IntVar[] queens = new IntVar[BoardSize];
for (int i = 0; i < BoardSize; ++i)
{
queens[i] = solver.MakeIntVar(0, BoardSize - 1, $"x{i}");
}
// Define constraints.
// All rows must be different.
solver.Add(queens.AllDifferent());
// All columns must be different because the indices of queens are all different.
// No two queens can be on the same diagonal.
IntVar[] diag1 = new IntVar[BoardSize];
IntVar[] diag2 = new IntVar[BoardSize];
for (int i = 0; i < BoardSize; ++i)
{
diag1[i] = solver.MakeSum(queens[i], i).Var();
diag2[i] = solver.MakeSum(queens[i], -i).Var();
}
solver.Add(diag1.AllDifferent());
solver.Add(diag2.AllDifferent());
// Create the decision builder to search for solutions.
DecisionBuilder db = solver.MakePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);
// Iterates through the solutions, displaying each.
int SolutionCount = 0;
solver.NewSearch(db);
while (solver.NextSolution())
{
Console.WriteLine("Solution " + SolutionCount);
for (int i = 0; i < BoardSize; ++i)
{
for (int j = 0; j < BoardSize; ++j)
{
if (queens[j].Value() == i)
{
Console.Write("Q");
}
else
{
Console.Write("_");
}
if (j != BoardSize - 1)
Console.Write(" ");
}
Console.WriteLine("");
}
SolutionCount++;
}
solver.EndSearch();
// Statistics.
Console.WriteLine("Statistics");
Console.WriteLine($" failures: {solver.Failures()}");
Console.WriteLine($" branches: {solver.Branches()}");
Console.WriteLine($" wall time: {solver.WallTime()} ms");
Console.WriteLine($" Solutions found: {SolutionCount}");
}
}Количество решений
Количество решений увеличивается примерно экспоненциально с размером платы:
| Размер платы | Решения | Время поиска всех решений (мс) |
|---|---|---|
| 1 | 1 | 0 |
| 2 | 0 | 0 |
| 3 | 0 | 0 |
| 4 | 2 | 0 |
| 5 | 10 | 0 |
| 6 | 4 | 0 |
| 7 | 40 | 3 |
| 8 | 92 | 9 |
| 9 | 352 | 35 |
| 10 | 724 | 95 |
| 11 | 2680 | 378 |
| 12 | 14200 | 2198 |
| 13 | 73712 | 11628 |
| 14 | 365596 | 62427 |
| 15 | 2279184 | 410701 |
Многие решения представляют собой просто вращения других, и для уменьшения объема необходимых вычислений можно использовать метод, называемый нарушением симметрии. Мы не используем это здесь; наше решение, представленное выше, не должно быть быстрым, оно простое. Конечно, мы могли бы сделать это намного быстрее, если бы хотели найти только одно решение вместо всех: не более нескольких миллисекунд для размеров доски до 50.

