ノイズの意味、ノイズが加わる場所、測定に及ぼす影響について学びます。
概要レポートは、集計可能レポートを集計した結果です。 集計可能レポートがコレクタでバッチ処理され、集計サービスによって処理されると、生成されるサマリー レポートにノイズ(ランダムな量のデータ)が追加されます。 ユーザーのプライバシーを保護するためにノイズが追加されます。このメカニズムの目的は、差分プライベートの測定をサポートできるフレームワークを用意することです。
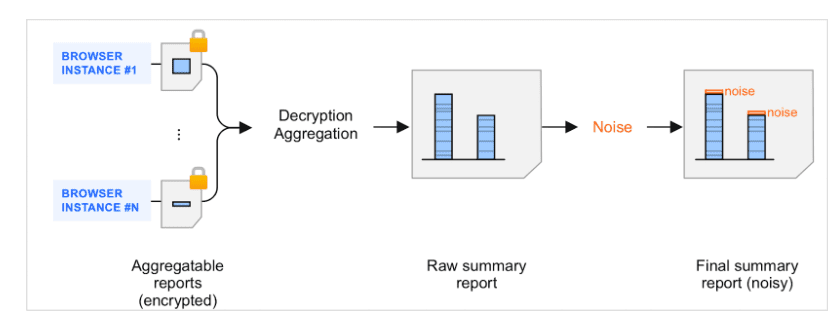
概要レポートのノイズの概要
現在の広告測定では、一般的にノイズの追加は考慮されていませんが、多くの場合、ノイズを追加しても結果の解釈には大きな違いはありません。
次のように考えると役立ちます。 特定のデータがノイズが多くなければ、そのデータに基づく決定を自信を持って行うことができますか?
たとえば、キャンペーン A では 15 件、キャンペーン B では 16 件だったという事実から、広告主はキャンペーンの戦略や予算を自信を持って変更できるでしょうか。
答えが「いいえ」の場合、ノイズは無関係です。
API の使用方法を次のように構成します。
- 上記の質問に対する答えは「はい」です。
- ノイズは、特定のデータに基づいて決定を下す能力に大きな影響を与えない方法で管理されています。次のようにアプローチできます。想定される最小コンバージョン数に対して、収集された指標のノイズを一定の割合未満に保ちます。
このセクションでは、2.
基本コンセプト
集計サービスは、概要レポートがリクエストされるたびに、各概要値に 1 回(キーごとに 1 回)ノイズを追加します。
これらのノイズ値は、以下で説明する特定の確率分布からランダムに取得されます。
ノイズに影響を与える要素はすべて、2 つの主要なコンセプトに依存します。
ノイズ分布(詳細は下記を参照)は、サマリー値が低か高かにかかわらず同じです。したがって、サマリー値が高いほど、この値と比較してノイズの影響が小さくなる可能性があります。
たとえば、合計購入額が $20,000 と合計購入額 $200 の両方が、同じ分布から選択されたノイズの影響を受けるとします。
この分布からのノイズが約 -100 ~+100 の範囲で変化するとします。
- まとめの購入額が $20,000 の場合、ノイズは 0 から 100÷20,000=0.5% の間で変動します。
- まとめの購入額が $200 の場合、ノイズは 0 ~ 100÷200=50% の間で変化します。
そのため、ノイズによる影響が $20,000 の合計購入額の場合、$200 の場合よりも小さくなる可能性があります。相対的に言えば、20,000 ドルの方がノイズが少なく、SN 比が高い可能性が高いです。
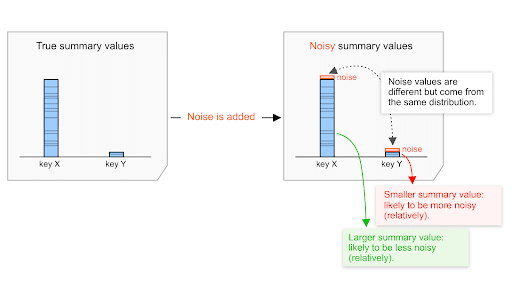
これには重要な実用的影響がいくつかあります。これについては、次のセクションで概説します。このメカニズムは API 設計の一部であり、実際的な影響は長期的です。広告テクノロジーがさまざまな集約戦略を設計、評価する際に、引き続き重要な役割を担うことになるでしょう。
ノイズは要約値に関係なく同じ分布から引き出されますが、その分布はいくつかのパラメータに依存します。これらのパラメータの一つであるイプシロンは、最終オリジン トライアル中に広告テクノロジーによって変更され、さまざまな有用性/プライバシーに関する調整を評価できます。ただし、イプシロンを調整する機能は一時的なものであると考えてください。ユースケースやうまく機能するイプシロンの値に関するフィードバックをぜひお寄せください。
広告テクノロジー企業はノイズの追加方法を直接管理することはできませんが、測定データに対するノイズの影響に影響を与えることはあります。次のセクションでは、ノイズが実際にどのような影響を与えるかを詳しく見ていきます。
その前に、ノイズがどのように適用されるかを詳しく見てみましょう。
ズームイン: ノイズの適用方法
1 つのノイズ分布
ノイズは、次のパラメータを使用してラプラス分布から引き出されます。
- 平均(
μ)は 0。つまり、最も可能性の高いノイズ値は 0(ノイズが追加されていない)であり、ノイズの多い値は元の値よりも小さくなる可能性が高い(バイアスがないと呼ばれることもあります)。 b = CONTRIBUTION_BUDGET/epsilonのスケール パラメータ。CONTRIBUTION_BUDGETはブラウザで定義されます。epsilonは集計サーバーで固定されています。
下の図は、μ=0、b = 20 のラプラス分布の確率密度関数を示しています。
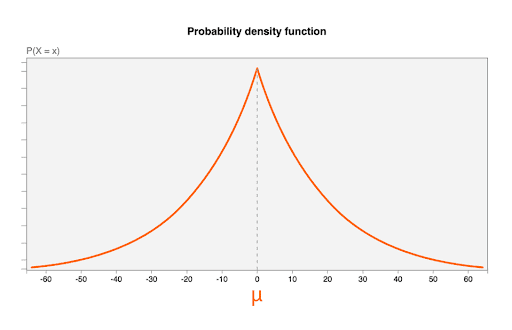
ランダムなノイズ値、1 つのノイズ分布
広告テクノロジーが 2 つの集計キー(key1 と key2)のサマリー レポートをリクエストしたとします。
集計サービスは、同じノイズ分布に従って 2 つのノイズ値 x1 と x2 を選択します。x1 が key1 のサマリー値に、x2 が key2 のサマリー値に加算されます。
図では、ノイズ値を同じものとして表しています。これは簡略化されています。実際には、ノイズ値は分布からランダムに取得されるため、変動します。
これは、ノイズ値がすべて同じ分布に由来し、適用先のサマリー値から独立していることを示しています。
ノイズのその他の特性
ノイズは、空の値(0)を含むすべてのサマリー値に適用されます。
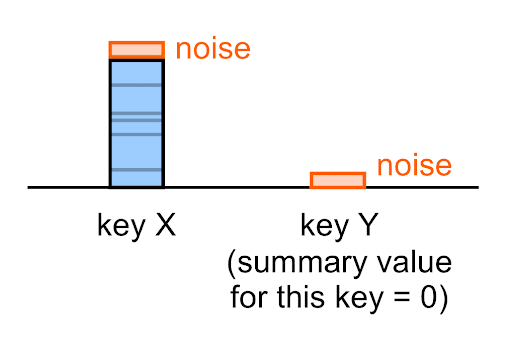
たとえば、あるキーの実際のサマリー値が 0 であっても、そのキーのサマリー レポートに表示されるノイズの多いサマリー値は(ほとんどの場合)0 ではありません。
ノイズには、正または負の数を指定できます。
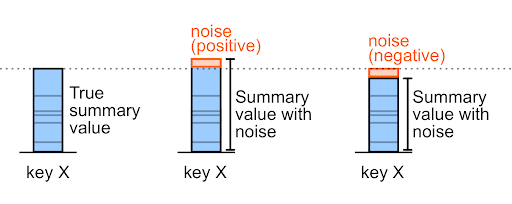
たとえば、事前ノイズの購入額が 327,000 の場合、ノイズは +6,000 または -6,000 になります(これらは任意の値の例です)。
ノイズの評価
ノイズの標準偏差の計算
ノイズの標準偏差は次のとおりです。
b*sqrt(2) = (CONTRIBUTION_BUDGET / epsilon)*sqrt(2)
例
イプシロン = 10 の場合、ノイズの標準偏差は次のようになります。
b*sqrt(2) = (CONTRIBUTION_BUDGET / epsilon)*sqrt(2) = (65,536/10)*sqrt(2) = 9,267
測定の差異が大きい場合に判断する
集計サービスによって出力された各値に加算されるノイズの標準偏差がわかっているため、比較に適したしきい値を決定し、観測された差がノイズによるものであるかどうかを判断できます。
たとえば、値に加わるノイズが約 +/- 10(スケーリングを考慮)で、2 つのキャンペーン間の値の差が 100 を超える場合、キャンペーン間で測定される値の差はノイズのみによるものではないと結論付けることができます。
Engage and share feedback
You can participate and experiment with this API.
- Read about aggregatable reports and the aggregation service, ask questions, and suggest feedback.
- Read the Attribution reporting guides.
- Ask questions and join discussions on the Privacy Sandbox Developer Support repo.
次のステップ
- 信号対雑音比を改善するためにどの変数を制御できるかについては、ノイズの使用をご覧ください。
- 集計レポート戦略の計画に役立つ情報として、概要レポートの設計上の決定事項をテストするをご覧ください。
- ノイズラボを試す。

